Длина | это… Что такое Длина?
Длина
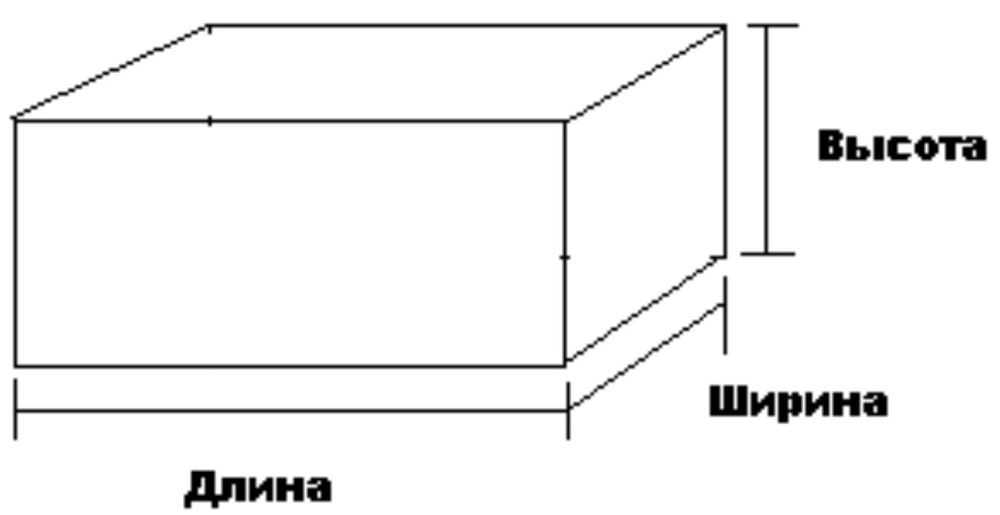
Длина — физическая величина, числовая характеристика протяжённости линий. В узком смысле под длиной понимают линейный размер предмета в продольном направлении (обычно это направление наибольшего размера), то есть расстояние между его двумя наиболее удалёнными точками, измеренное горизонтально, в отличие от высоты, которая измеряется в вертикальном направлении, а также ширины или толщины, которые измеряются поперёк объекта (под прямым углом к длине). В физике термин «длина» обычно используется как синоним «расстояния» и обозначается или .
Размерность длины — dim l = L. В ряду других пространственных величин длина — это величина единичной размерности, тогда как площадь — двухмерная, объём — трёхмерная. В большинстве систем измерений единица длины — одна из фундаментальных единиц измерения, на основе которых образуются другие единицы. В международной системе единиц (СИ) за единицу длины принят метр.
Содержание
|
Единицы измерения длины
Относительные размеры
объектов, м.
-20 —
–
-18 —
–
-16 —
–
-14 —
–
-12 —
–
-10 —
–
-8 —
–
-6 —
–
-4 —
–
-2 —
–
0 —
–
2 —
–
4 —
–
6 —
–
8 —
–
10 —
–
12 —
–
14 —
–
16 —
–
18 —
–
20 —
–
22 —
–
24 —
–
26 —
–
28 —
–
30 —
←
Диаметр протона — 0,8·10-15
←
Диаметр атомного ядра — 3·10-15
←
Размер атома — 3·10-10
←
Размер водяной капли
в тумане — 5·10-6
←
Средний рост человека — 1,7·100
←
Диаметр Луны — 3,48·106
←
Диаметр Земли — 1,3·107
←
Радиус орбиты Луны — 3,84·108
←
Диаметр Солнца — 1,39·109
←
Средний радиус
орбиты Земли — 1,5·1011
←
Расстояние до
звезды альфа Центавра — 4·1016
←
Диаметр Млечного Пути — 7·1020
←
Расстояние до
туманности Андромеды — 1022
←
Размер видимой Вселенной — 1026
Метрическая система
Метрическая система считается самой удобной из всех придуманных из-за своей простоты.
В основе метрической системы лежит единица измерения метр. Все остальные единицы измерения являются кратными степеням десяти от метра (например, километр — это 10³ метров и т. п.), что позволяет облегчить подсчёты. До 1960 года у метра был специальный эталон, ныне хранящийся в Париже. Сегодня, по определению, метр равен расстоянию, которое проходит свет в вакууме за 1/299 792 458 долю секунды.
Британская/Американская система
Исходными английскими мерами длины были миля, ярд, фут и дюйм. Миля пришла в Англию из Древнего Рима, где она определялась как тысяча двойных шагов вооружённого римского воина.
- Лига (лье)
- Фурлонг
- Чейн
- Род
- Линк
- Ладонь
- Линия
Старорусская система
В Древней Руси мерой длины, веса и т. п. являлся человек. На это указывают названия мер длины: локоть (расстояние от конца вытянутого среднего пальца руки или сжатого кулака до локтевого сгиба), пядь (расстояние между вытянутым большим и указательным пальцами руки), сажень (расстояние от конца пальцев одной руки до конца пальцев другой) и другие[1].
В частности, аршин был связан с длиной человеческого шага. Однако необходимость унификации систем измерений с британской в связи с развитием международной торговли потребовала введения во времена Петра I так называемого «казённого аршина». Это была мерная линейка с металлическими наконечниками с государственным клеймом. Казённый аршин равнялся 28 английским дюймам и делился на 16 вершков.[2]
См. также
- Миля
- Межевая верста
- Верста
- Косая сажень
- Маховая сажень
- Пядь
Древнегреческая система
- Дактиль (единица измерения)
- Кондилос
- Оргия
- Палайста
- Пекис
- Плетр
- Подес
- Стадий, или «стадия»
- Эпидама
Мусульманская система
- Ангушт или Асба (аналог дюйма)
- Пай (аналог фута)
- Ба или кама, равная приблизительно 2 м
- Касаба или наб
- Фарсах или парасанг, равный трём милям по 1000 Ба, или 6 км
- Барид, равный четырём фарсахам[3]
Типографическая система
- Цицеро
- Пункт
Морская система
Морская система измерения длины привязана к размеру планеты Земля.
В качестве основной единицы измерения принята морская миля, равная длине одной минуты (1/60 градуса) дуги меридиана земного эллипсоида. Длина морской мили является величиной переменной, зависящей от широты. Ее численное значение составляет от 1843 метров на экваторе до 1861,6 метров на полюсах.
Международная морская миля составляет 1852 м, в отличие от морской мили Британской системы (1853,184 м). Для измерения меньших размеров применяют кабельтов — 1/10 морской мили, или 185,2 м (округлённо — 185 м).[4]
Единицы, применяемые в астрономии
- Астрономическая единица
- Световой год
- Парсек
Измерительные инструменты и меры
- Линейка
- Концевая мера
- Штангенинструмент
- Рулетка (инструмент)
- Микрометр (инструмент)
- Индикатор часового типа
- Калибр (инструмент)
- Толщиномер
Измерительные приборы
- Высотомер
- Радиовысотомер
- Дальномер
- Радиодальномер
- Интерференционные толщиномеры (ультразвуковые, лазерные, радиационные)
Другие средства
- Большие расстояния в навигации определяются при помощи средств радионавигационных систем или спутниковых систем
- Очень маленькие расстояния измеряются с помощью измерительных микроскопов
См.
также- Длина кривой
- Мера
- Объём
- Площадь
- Высота
- Глубина
Примечания
- ↑ Меры длины
- ↑ Отечественные компании переходят на исторические меры длины
- ↑ Власов А.Д., Мурин Б.П. Единицы физических величин в науке и технике: Справочник. — М.: Энергоатомиздат, 1990. — С. 176. — ISBN 5-283-03966-8
- ↑ Учебник по навигации
Wikimedia Foundation. 2010.
Высота, Ширина, Длина Или Объём Объекта ответы
Высота, Ширина, Длина Или Объём Объекта ответы. Обновленные и проверенные решения для всех уровней CodyCross Исполнительские искусства группа 886
Ответ
Высота, ширина, длина или объём объекта Ответ
Р А З М Е Р
Балка Для Строительства Лестничных Пролётов
Некрупная Альтернатива Бассейну В Бане
CodyCross Исполнительские искусства группа 886
CodyCross Исполнительские искусства группа 886 ответы
| определение | Ответ |
|---|---|
| Индейское Племя, Владеющее Каньоном Антилопы | навахо |
| Ей К Лицу , Фильм Р Земекиса | смерть |
| Некрупная Альтернатива Бассейну В Бане | купель |
| Высота, Ширина, Длина Или Объём Объекта | размер |
| Балка Для Строительства Лестничных Пролётов | косоур |
| Бумаги, Которые Коллекционирует Скрипофил | ценные |
| Любимое Занятие Книжных Червей | чтение |
| В Его Басне Ворона Ротозейка Лишилась Сыра | крылов |
| Накладка Из Волос, Популярная У Женщин В 1960 Х | шиньон |
| Футбол С Мячом Почти Два Метра В Диаметре | пушбол |
| Длинный Зелёный Овощ Для Засолки И Маринования | огурец |
| Этот Гарри Не Волшебник, Но Тоже Поражал Чудесами | гудини |
| Ускоряющееся Движение Самолёта По Взлётной Полосе | разбег |
| Часть Пищевода Лужёная | глотка |
| Библейское Судно Для Спасения Пар От Потопа | ковчег |
следующий
Планета Земля Подводный мир Изобретения Времена года В цирке Транспорт Кулинарное искусство Спорт Фауна и Флора Древний Египет Парк развлечений Средневековье Париж Казино В библиотеке Научная лаборатория На дворе 70-е Зоомагазин Нью-Йорк, Нью-Йорк! В кинотеатре Прекрасный Рим Дикий Запад В аэропорту На ферме Лондон В универмаге Показ мод На курорте Удивительная Япония Концертный зал Телестудия Дом, милый дом Круизный лайнер Греция Мир маленьких вещей Путешествуем на поезде Музей искусств Аквапарк Тур по Бразилии Восьмидесятые Время СПА Приключения в кемпинге Поездка в Испанию Вымышленный мир Освоение космоса Студенческая жизнь Игры
— Какая разница между шириной и высотой?
спросил
Изменено 8 лет, 10 месяцев назад
Просмотрено 21к раз
$\begingroup$
Я никогда не был хорош в математике.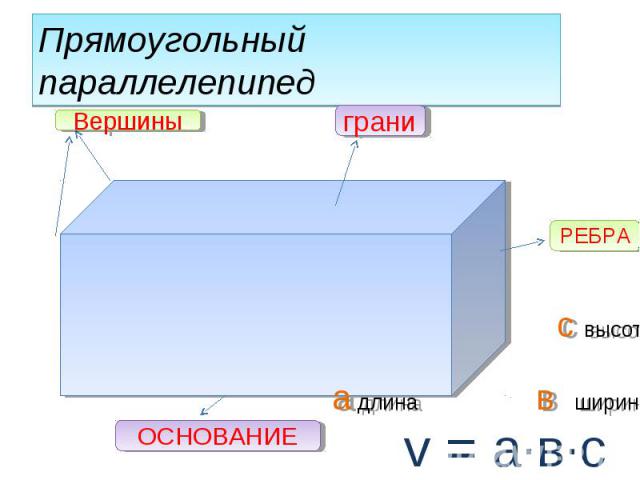
.. Я хочу изменить это, поскольку разработка игр всегда была моей страстью. Я начал изучать математику в Академии Хана около месяца назад, и до этого момента все было понятно (https://www.khanacademy.org/math/cc-sixth-grade-math/cc-6th-geometry-topic/ cc-6-я-площадь/v/площадь-параллелограмма). Насколько я понимаю, он измеряет площади двух треугольников и получает площадь параллелограмма. Мне трудно понять это из-за…
Насколько высота этого пареллелограмма отличается от его ширины? Я всегда думал, что A=l w и A=b h всегда одинаковы? На изображении вы можете видеть высоту 6 см, длину 8 см и основание 10 см. Почему высота не равна 8 см, как ширина?
Пожалуйста, объясните это так, чтобы я мог понять. Большое спасибо за ваше время.
- площадь
- геометрия
$\endgroup$
6
$\begingroup$
Два анекдота, которые я рассказываю своим ученикам (хотя лично я рассказываю им лучше), когда возникает путаница между шириной и высотой (не расстраивайтесь.
.. такое случается часто!):
Парень наткнулся на своего приятеля посреди поля, отчаянно пытавшегося прижать складную рулетку к далеко недоступной вершине торчащего из земли столба. Парень спрашивает: «Если это так важно, то почему бы вам просто не опрокинуть шест и не измерить его, пока он лежит на земле?» Его приятель ответил: «Потому что… я хочу знать, как высокий он, а не длинный !»
и
Пилоту и второму пилоту пришлось совершить аварийную посадку на незнакомой взлетно-посадочной полосе. «Мы приближаемся слишком быстро!» предупредил второго пилота: «Мы выбежим за пределы взлетно-посадочной полосы!» Пилот отрегулировал закрылки и угол захода на посадку, чтобы снизить скорость и выиграть время. «Недостаточно!» — сказал второй пилот. — Мы все равно выбежим из взлетно-посадочной полосы! Пилот сделал еще корректировки, и еще раз, но второй пилот все еще был в бешенстве: «Мы собираемся вылететь за взлетно-посадочную полосу!» Совершив последний подвиг аэродинамической магии, искусный пилот сумел снизить скорость захода на посадку так, что аппарат очень мягко приземлился и вырулил на безопасную и надежную остановку носом 9.
0017 только за концом взлетно-посадочной полосы. — Маноман, — вздохнул измученный пилот. «Это самая короткая взлетно-посадочная полоса, которую я когда-либо встречал!» «Ага, — согласился второй пилот, — но посмотрите, какой он в ширину !»
0017 только за концом взлетно-посадочной полосы. — Маноман, — вздохнул измученный пилот. «Это самая короткая взлетно-посадочная полоса, которую я когда-либо встречал!» «Ага, — согласился второй пилот, — но посмотрите, какой он в ширину !»… и именно поэтому, друзья мои, я всегда стараюсь формулировать формулу площади параллелограмма как «основание-высота».
Важно отметить, что в формуле «база-время-высота» «база» — это действительно любая выбранная вами сторона, а «высота» — это высота, перпендикулярная выбранной базе 92$.
$\endgroup$
$\begingroup$
Надеюсь, эта аналогия поможет,
площадь всех параллелограммов равна
А = основание * высота,
где высота — это длина перпендикуляра от основания параллелограмма до его вершины.
Итак, прямоугольник представляет собой особого типа параллелограмм, все стороны которого образуют прямые углы.
Следовательно, ширина прямоугольника фактически равна перпендикулярен от его основания к его вершине.
Таким образом, для прямоугольников мы можем использовать формулу
.А = длина * ширина.
Примечание. Я думаю, что ширина, длина, основание и высота в данном случае определены довольно свободно, но я надеюсь, что вы поняли общее представление. Вы можете назвать длину прямоугольника «базой», а его ширину «высотой», если хотите. Это, вероятно, позволит избежать путаницы.
$\endgroup$
$\begingroup$ 92$ (где 80$ получается как 8*10$)?
Если да, то представьте, что произошло бы, если бы параллелограмм наклонялся все больше и больше; если хотите, представьте это как раму, которую вы держите так, что ее нижняя часть опирается на землю, но боковые стороны наклонены (может быть, из-за того, что винты, соединяющие их с верхней и нижней частью, недостаточно затянуты или что-то в этом роде).
В конце концов все это рухнет, и верх тоже будет лежать на земле.
Тогда все это вообще не будет занимать никакой площади!
Таким образом, не «ширина» (длина сторон) определяет, какая площадь находится между верхом и низом кадра; важно, насколько верхняя часть кадра находится над нижней.
$\endgroup$
5
$\begingroup$
Меня всегда смущали такие термины, как высота и ширина. Попробуйте посмотреть на это так. Вы можете работать с ним, используя более знакомые понятия квадратов и треугольников. Например, вы знаете гипотенузу прямоугольного треугольника и одну сторону прямоугольного треугольника, поэтому можете использовать теорему Пифагора, чтобы найти длину другой стороны. Отсюда можно найти длину длинной стороны прямоугольника. У вас уже есть длина другой стороны. Из всей этой информации можно сделать вывод, что площадь равна площади прямоугольника плюс удвоенная площадь одного из треугольников (поскольку они одинаковы).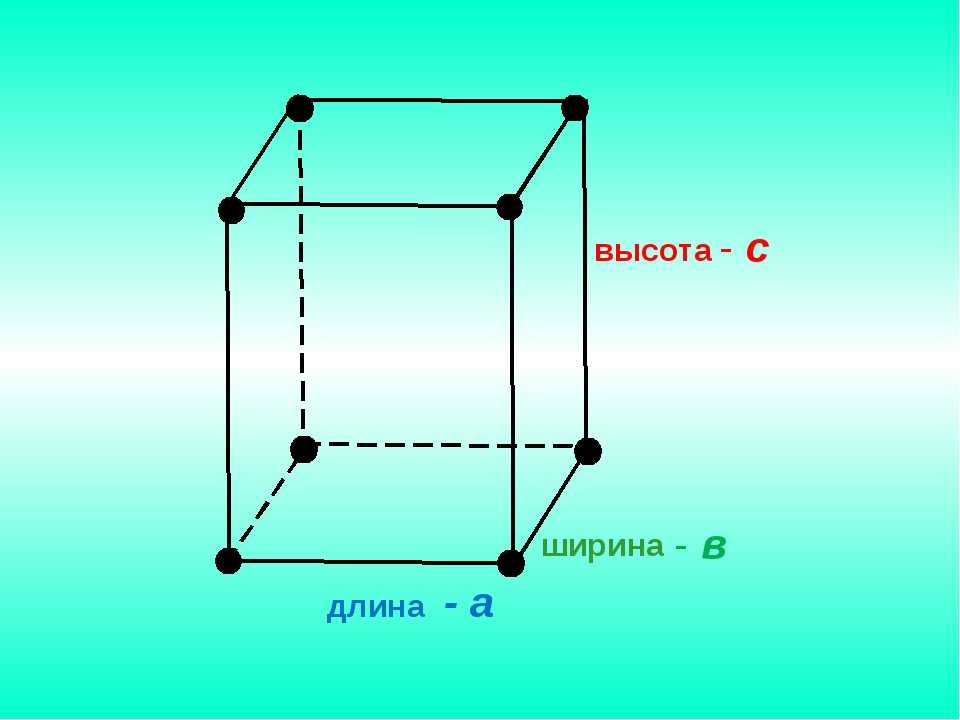
$\endgroup$
1
Как рассчитать объем, длину, ширину и высоту прямоугольного параллелепипеда | Калькулятор Nickzom
Изображение выше представляет прямоугольный параллелепипед.
Для вычисления объема прямоугольного параллелепипеда требуются три основных параметра: длина, ширина и высота прямоугольного параллелепипеда.
Формула для вычисления объема прямоугольного параллелепипеда:
V = lwh
Где:
V = Объем прямоугольного параллелепипеда
l = Длина прямоугольного параллелепипеда
w = Ширина прямоугольного параллелепипеда
h = Высота прямоугольного параллелепипеда
Решим пример
Найдите объем прямоугольного параллелепипеда длиной 6 см, ширина 2 см и высота 10 см.
Отсюда следует, что:
l = длина параллелепипеда = 6
w = ширина параллелепипеда = 2
h= = высота параллелепипеда = 10
V = lwh
V = 6 x 2 x 10
V = 120
Таким образом, объем прямоугольного параллелепипеда это 120 см 3 .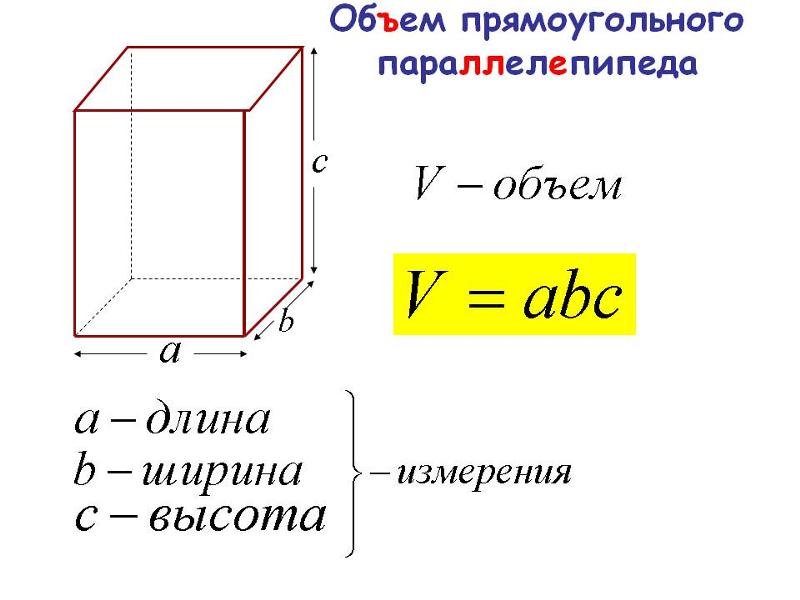
Расчет длины прямоугольного параллелепипеда по данным объема, ширины и высоты
Формула l = V / (w)(h)
Где;
V = Объем прямоугольного параллелепипеда
l = Длина параллелепипеда
w = Ширина прямоугольного параллелепипеда
h = Высота прямоугольного параллелепипеда
Решим пример:
Найдите длину прямоугольного параллелепипеда с объемом 440 см 3 , шириной 5 см и высотой 11 см.
Это означает, что;
V = объем параллелепипеда = 440 см 3
w = ширина параллелепипеда = 5 см
h = высота параллелепипеда = 11 см
l = V / (w)(h)
l = 440 / (5)(11)
l = 440 / 55
l = 8 см
Следовательно, 2 2 90 см003.
Вычисление ширины прямоугольного параллелепипеда по данным объема, длины и высоты
Формула w = В / (l)(h)
Где;
V = Объем прямоугольного параллелепипеда
l = Длина прямоугольного параллелепипеда
w = Ширина прямоугольного параллелепипеда
h = Высота прямоугольного параллелепипеда
Давайте решим пример:
Найдите ширину прямоугольного параллелепипеда с объемом 180 см 3 , длиной 6 см и высотой 10 см
Это означает, что;
V = объем прямоугольного параллелепипеда = 180 см 3
l = длина параллелепипеда = 6 см
h = высота параллелепипеда = 10 см
W = V / (L) (H)
W = 180 / (6) (10)
W = 180 / 60
W = 3 ,
W = 3 7,
W = 3
W = .
ширина прямоугольного параллелепипеда равна 3 см. Расчет высоты прямоугольного параллелепипеда по данным объема, длины и ширины
Формула h = V / (l)(w)
Где;
V = Объем прямоугольного параллелепипеда
l = Длина прямоугольного параллелепипеда
w = ширина кубоида
h = высота параллелепипеда
Давайте решим пример:
Найдите высоту прямоугольного параллелепипеда с объемом 195 см 3 , длиной 5 см и шириной 3 см
Это означает, что;
V = объем прямоугольного параллелепипеда = 195 см 3
l = длина параллелепипеда = 5 см
w = ширина параллелепипеда = 3 см
h = V / (l)(w)
h = 195 / (5)(3)
h = 195 / 15
h = 13 см
Следовательно, высота параллелепипеда равна 13 см.
Калькулятор Никзома – Энциклопедия калькуляторов способна вычислить объем прямоугольного параллелепипеда.
Чтобы получить ответ и вычисления объема прямоугольного параллелепипеда, используйте Калькулятор Никзома – Энциклопедия калькуляторов. Во-первых, вам нужно получить приложение.
Вы можете получить это приложение любым из следующих способов:
Web – https://www.nickzom.org/calculator-plus
Чтобы получить доступ к профессиональной версии через Интернет, вам необходимо зарегистрироваться и подписаться за NGN 1,500 9036 за 9006 иметь полный доступ ко всем функциям.
Вы также можете попробовать демо-версию через https://www.nickzom.org/calculator
Android (платная) – https://play.google.com/store/apps/details?id=org .nickzom.nickzomcalculator
Android (бесплатно) – https://play.google.com/store/apps/details?id=com.nickzom.nickzomcalculator
Apple (платно) – https://itunes.