«Самарский Стройфарфор» внедряет «турбо эффект»
«Ringo» считается настоящей «жемчужиной» коллекции сантехнических изделий завода. Сидение с оригинальной крышкой с системой плавного опускания, особое покрытие «SANITA CRYSTAL» свидетельствуют об изысканности данной модели. И вот теперь еще одна инновация в пользу «аристократа» – мощная система слива, визуально напоминающая турбо эффект.
«Полезная модель унитаза № 160526», как называется запатентованная разработка, состоит из трех основных элементов: чаши, сифона и сопла подачи воды в сифон. Примечательно, что сифон, канал подвода воды и сопло, имеющее форму трубки, выполнены в форме единой неразъемной керамической детали. Расположен канал подвода воды непосредственно под сифоном. Модель включает в себя гидравлическую, пневматическую и электрическую системы, обеспечивающие автономное функционирование сантехнического изделия при использовании.
В отличие от системы смыва в обычном унитазе, где подача воды идет стандартным образом сверху, в новой модификации унитаза «Ringo» вода поступает еще и снизу.
Необходимость в данной разработке связана с возросшим уровнем требований со стороны потребителей к качеству санитарно-технических изделий, и с такой важнейшей характеристикой как эффективность слива. Специалисты предприятия поставили цель – увеличить эту характеристику за счёт доработок.
Эффективность слива проверяется в специальных условиях с помощью пластиковых шариков. Согласно ГОСТу допускается определенный процент остатка. В качестве эксперимента смывали разные материалы: куски пенопласта, металлические шарики. Система слива в полезной модели унитаза № 160525, основанная на принципе эжекции, прекрасно справлялась с заданиями, показывая стопроцентный результат.
Руководителем проекта и автором идеи по созданию универсальной модели «Ringo» является заместитель генерального директора Алексей Бузунов. В соавторстве с ним над проектом работали инженеры-конструкторы сектора исследовании: Игорь Чапин, Виктор Пекшев и Виталий Серёгин.
Работа началась еще в 2013 году. Около года ушло на теоретические и экспериментальные исследования, разработку концепции. Еще полгода – на создание модели. После серии успешных испытаний 17 ноября 2015 года предприятие подало заявку на патент; 25 февраля 2016 года Полезная модель унитаза № 160526 была зарегистрирована Федеральной службой по интеллектуальной собственности Роспатентом.
Однако с получением документа, подтверждающего авторство, работа над моделью не закончились. Сейчас инженеры занимаются гидравликой и электрической автоматикой, работают над надежностью оборудования, которым снабжены унитазы «Ringo», а также минимизацией его технического обслуживания.
– Наша задача – усовершенствовать оборудование, чтобы сделать систему удобной с точки зрения эксплуатации. – Заявили разработчики. – В идеале хотим получить встроенный унитаз с автоматикой, которая монтируется в стене и не требует вмешательства извне. А это значит, что изделие должно быть надежным и способным к эксплуатации на долгие годы.
Комментарии:
Игорь Чапин, инженер-конструктор сектора исследований:
– Всё, что модернизируется и улучшается, становится дороже. Специалисты завода как раз работают над тем, чтобы снизить себестоимость Полезной модели унитаза № 160526, сделать конечную цену на изделие более доступной и привлекательной для потребителя. Мы уходим от дорогостоящих элементов, ищем более простые, стандартные, чтобы минимизировать расходы.
Виктор Пекшев, инженер-конструктор сектора исследований:
– В модели заложены возможности регулировки подачи воды.
Подача воды сверху регулируется вручную за счет стандартной арматуры. Подачу воды снизу регулирует автоматика – здесь важно, чтобы пользователь изначально, еще до эксплуатации сантехнического изделия, задал необходимые временные параметры. Когда модель выйдет в серийное производство, выпустят инструкцию, где будет указано, как осуществлять регулировку подачи.
ОглавлениеОТ ИЗДАТЕЛЬСТВАИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ ВВЕДЕНИЕ Глава I. Кинематика § 1. Движение тел § 2. Кинематика. Относительность движения и покоя. § 3. Траектория движения § 4.  § 5. Движение точки § 6. Описание движения точки § 7. Измерение длины § 8. Измерение промежутков времени § 9. Равномерное прямолинейное движение и его скорость § 10. Знак скорости при прямолинейном движении § 11. Единицы скорости § 12. Графики зависимости пути от времени § 13. Графики зависимости скорости от времени § 14. Неравномерное прямолинейное движение § 15. Мгновенная скорость § 16. Ускорение при прямолинейном движении § 17. Скорость прямолинейного равноускоренного движения § 18. Знак ускорения при прямолинейном движении § 19. Графики скорости при прямолинейном равноускоренном движении § 20. Графики скорости при произвольном неравномерном движении § 21. Нахождение пути, пройденного при неравномерном движении, при помощи графика скорости § 22. Путь, пройденный при равнопеременном движении § 23. Векторы § 24. Разложение вектора на составляющие § 25. Криволинейное движение § 26.  Скорость криволинейного движения§ 27. Ускорение при криволинейном движении § 28. Движение относительно разных систем отсчета § 29. Кинематика космических движений Глава II. Динамика § 30. Задачи динамики § 31. Закон инерции § 32. Инерциальные системы отсчета § 33. Принцип относительности Галилея § 34. Силы § 35. Уравновешивающиеся силы. О покое тела и о движении по инерции § 36. Сила — вектор. Эталон силы § 37. Динамометры § 38. Точка приложения силы § 39. Равнодействующая сила § 40. Сложение сил, направленных по одной прямой § 41. Сложение сил, направленных под углом друг к другу § 42. Связь между силой и ускорением § 43. Масса тела § 44. Второй закон Ньютона § 45. Единицы силы и массы § 46. Системы единиц § 47. Третий закон Ньютона § 48. Примеры применения третьего закона Ньютона § 50. Система тел. Закон сохранения импульса § 51. Применения закона сохранения импульса § 52.  Свободное падение тел§ 53. Ускорение свободного падения § 54. Падение тела без начальной скорости и движение тела, брошенного вертикально вверх § 55. Вес тела § 56. Масса и вес § 57. Плотность вещества § 58. Возникновение деформаций § 59. Деформации в покоящихся телах, вызванные действием только сил, возникающих при соприкосновении § 60. Деформации в покоящихся телах, вызванные силой тяжести § 61. Деформации тела, испытывающего ускорение § 62. Исчезновение деформаций при падении тел § 63. Разрушение движущихся тел § 64. Силы трения § 65. Трение качения § 66. Роль сил трения § 67. Сопротивление среды § 68. Падение тел в воздухе Глава III. Статика § 69. Задачи статики § 70. Абсолютно твердое тело § 71. Перенос точки приложения силы, действующей на твердое тело § 72. Равновесие тела под действием трех сил § 73. Разложение сил на составляющие § 74. Проекции сил. Общие условия равновесия § 75. Связи.  Силы реакции связей. Тело, закрепленное на оси§ 76. Равновесие тела, закрепленного на оси § 77. Момент силы § 78. Измерение момента силы § 79. Пара сил § 80. Сложение параллельных сил. Центр тяжести § 81. Определение центра тяжести тел § 82. Различные случаи равновесия тела под действием силы тяжести § 83. Условия устойчивого равновесия под действием силы тяжести § 84. Простые машины § 85. Клин и винт Глава IV. Работа и энергия § 86. «Золотое правило» механики § 87. Применения «золотого правила» § 88. Работа силы § 89. Работа при перемещении, перпендикулярном к направлению силы § 91. Положительная и отрицательная работа § 92. Единица работы § 93. О движении по горизонтальной плоскости § 94. Работа силы тяжести при движении по наклонной плоскости § 95. Принцип сохранения работы § 96. Энергия § 97. Потенциальная энергия § 98. Потенциальная энергия упругой деформации § 99.  Кинетическая энергия§ 100. Выражение кинетической энергии через массу и скорость тела § 101. Полная энергия тела § 102. Закон сохранения энергии § 103. Силы трения и закон сохранения механической энергии § 104. Превращение механической энергии во внутреннюю энергию § 105. Всеобщий характер закона сохранения энергии § 106. Мощность § 107. Расчет мощности механизмов § 108. Мощность, быстроходность и размеры механизма § 109. Коэффициент полезного действия механизмов Глава V. Криволинейное движение § 110. Возникновение криволинейного движения § 111. Ускорение при криволинейном движении § 112. Движение тела, брошенного в горизонтальном направлении § 113. Движение тела, брошенного под углом к горизонту § 114. Полет пуль и снарядов § 115. Угловая скорость § 116. Силы при равномерном движении по окружности § 117. Возникновение силы, действующей на тело, движущееся по окружности § 118. Разрыв маховиков § 119. Деформация тела, движущегося по окружности § 120.  «Американские горк軧 121. Движение на закруглениях пути § 122. Движение подвешенного тела по окружности § 123. Движение планет § 124. Закон всемирного тяготения § 125. Искусственные спутники Земли Глава VI. Движение в неинерциальных системах отсчета и силы инерции § 126. Роль системы отсчета § 127. Движение относительно разных инерциальных систем отсчета § 128. Движение относительно инерциальной и неинерциальной систем отсчета § 129. Поступательно движущиеся неинерциальиые системы § 130. Силы инерции § 131. Эквивалентность сил инерции и сил тяготения § 132. Невесомость и перегрузки § 133. Является ли Земля инерциальиой системой отсчета? § 134. Вращающиеся системы отсчета § 135. Силы инерции при движении тела относительно вращающейся системы отсчета § 136. Доказательство вращения Земли § 137. Приливы Глава VII. Гидростатика § 138. Подвижность жидкости § 139. Силы давления § 140. Измерение сжимаемости жидкости § 141.  «Несжимаемая» жидкость§ 142. Силы давления в жидкости передаются во все стороны § 143. Направление сил давления § 144. Давление § 145. Мембранный манометр § 146. Независимость давления от ориентации площадки § 147. Единицы давления § 148. Определение сил давления по давлению § 149. Распределение давления внутри жидкости § 150. Закон Паскаля § 151. Гидравлический пресс § 152. Жидкость под действием силы тяжести § 153. Сообщающиеся сосуды § 154. Жидкостный манометр § 155. Устройство водопровода. Нагнетательный насос § 156. Сифон § 157. Сила давления на дно сосуда § 158. Давление воды в морских глубинах § 159. Прочность подводной лодки § 160. Закон Архимеда § 161. Измерение плотности тел на основании закона Архимеда § 162. Плавание тел § 163. Плавание несплошных тел § 164. Устойчивость плавания кораблей § 165. Всплывание пузырьков § 166. Тела, лежащие на дне сосуда Глава VIII. Аэростатика § 167.  Механические свойства газов§ 168. Атмосфера § 169. Давление атмосферы § 170. Другие опыты, показывающие существование атмосферного давления § 171. Разрежающие насосы § 172. Влияние атмосферного давления на уровень жидкости в трубке § 173. Максимальная высота столба жидкости § 174. Опыт Торричелли. Ртутный барометр и барометр-анероид § 175. Распределение атмосферного давления по высоте § 176. Физиологическое действие пониженного давления воздуха § 177. Закон Архимеда для газов § 178. Воздушные шары и дирижабли § 179. Применение сжатого воздуха в технике Глава IX. Гидродинамика и аэродинамика § 180. Давление в движущейся жидкости § 181. Течение жидкости по трубам § 182. Закон Бернулли § 183. Жидкость в неинерциальных системах отсчета § 184. Реакция движущейся жидкости и ее использование § 185. Перемещение на воде § 186. Ракеты § 187. Реактивные двигатели § 188. Баллистические ракеты § 189. Взлет ракеты с Земли § 190.  Сопротивление воздуха§ 191. Эффект Магиуса и циркуляция § 192. Подъемная сила крыла и полет самолета § 193. Турбулентность в потоке жидкости или газа § 194. Ламинарное течение РАЗДЕЛ ВТОРОЙ. ТЕПЛОТА. МОЛЕКУЛЯРНАЯ ФИЗИКА Глава X. Тепловое расширение твердых и жидких тел § 195. Тепловое расширение твердых и жидких тел § 196. Термометры § 197. Формула линейного расширения § 198. Формула объемного расширения § 199. Связь между коэффициентами линейного и объемного расширения § 200. Измерение коэффициента объемного расширения жидкостей § 201. Особенности расширения воды Глава XI. Работа. Теплота. Закон сохранения энергии § 202. Изменения состояния тел § 203. Нагревание тел при совершении работы § 204. Изменение внутренней энергии тел при теплопередаче § 205. Единицы количества теплоты § 206. Зависимость внутренней энергии тела от его массы и вещества § 207. Теплоемкость тела § 208. Удельная теплоемкость § 209.  Калориметр. Измерение теплоемкостей§ 210. Закон сохранения энергии § 211. Невозможность «вечного двигателя» § 212. Различные виды процессов, при которых происходит передача теплоты Глава XII. Молекулярная теория § 213. Молекулы и атомы § 214. Размеры атомов и молекул § 215. Микромир § 216. Внутренняя энергия с точки зрения молекулярной теории § 217. Молекулярное движение § 218. Молекулярное движение в газах, жидкостях и твердых телах § 219. Броуновское движение § 220. Молекулярные силы Глава XIII. Свойства газов § 221. Давление газа § 222. Зависимость давления газа от температуры § 223. Формула, выражающая закон Шарля § 224. Закон Шарля с точки зрения молекулярной теории § 225. Изменение температуры газа при изменении его объема. Адиабатические и изотермические процессы § 226. Закон Бойля — Мариотта § 227. Формула, выражающая закон Бойля — Мариотта § 228. График, выражающий закон Бойля — Мариотта § 229. 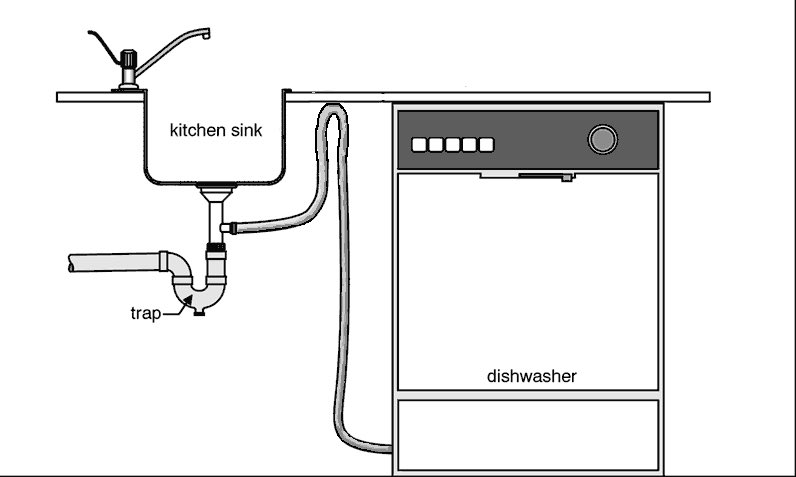 Зависимость между плотностью газа и его давлением§ 230. Молекулярное толкование закона Бойля — Мариотта § 231. Изменение объема газа при изменении температуры § 232. Закон Гей-Люссака § 233. Графики, выражающие законы Шарля и Гей-Люссака § 234. Термодинамическая температура § 235. Газовый термометр § 236. Объем газа и термодинамическая температура § 237. Зависимость плотности газа от температуры § 238. Уравнение состояния газа § 239. Закон Дальтона § 240. Плотность газов § 241. Закон Авогадро § 242. Моль. Постоянная Авогадро § 243. Скорости молекул газа § 244. Об одном из способов измерения скоростей движения молекул газа (опыт Штерна) § 245. Удельные теплоемкости газов § 246. Молярные теплоемкости § 247. Закон Дюлонга и Пти Глава XIV. Свойства жидкостей § 248. Строение жидкостей § 249. Поверхностная энергия § 250. Поверхностное натяжение § 251. Жидкостные пленки § 252. Зависимость поверхностного натяжения от температуры § 253.  Смачивание и несмачивание§ 254. Расположение молекул у поверхности тел § 255. Значение кривизны свободной поверхности жидкости § 256. Капиллярные явления § 257. Высота поднятия жидкости в капиллярных трубках § 258. Адсорбция § 259. Флотация § 260. Растворение газов § 261. Взаимное растворение жидкостей § 262. Растворение твердых тел в жидкостях Глава XV. Свойства твердых тел. Переход тел из твердого состояния в жидкое § 263. Введение § 264. Кристаллические тела § 265. Аморфные тела § 266. Кристаллическая решетка § 267. Кристаллизация § 268. Плавление и отвердевание § 269. Удельная теплота плавления § 270. Переохлаждение § 271. Изменение плотности веществ при плавлении § 272. Полимеры § 273. Сплавы § 274. Затвердевание растворов § 275. Охлаждающие смеси § 276. Изменения свойств твердого тела Глава XVI. Упругость и прочность § 277. Введение § 278. Упругие и пластические деформации § 279.  Закон Гука§ 280. Растяжение и сжатие § 281. Сдвиг § 282. Кручение § 283. Изгиб § 284. Прочность § 285. Твердость § 286. Что происходит при деформации тел § 287. Изменение энергии при деформации тел Глава XVII. Свойства паров § 288. Введение § 289. Пар насыщенный и ненасыщенный § 290. Что происходит при изменении объема жидкости и насыщенного пара § 291. Закон Дальтона для пара § 292. Молекулярная картина испарения § 293. Зависимость давления насыщенного пара от температуры § 294. Кипение § 295. Удельная теплота парообразования § 296. Охлаждение при испарении § 297. Изменение внутренней энергии при переходе вещества из жидкого состояния в парообразное § 298. Испарение при кривых поверхностях жидкости § 299. Перегревание жидкости § 300. Пересыщение паров § 301. Насыщение пара при возгонке § 302. Превращение газа в жидкость § 303. Критическая температура § 304. Сжижение газов в технике § 305.  Вакуумная техника§ 306. Водяной пар в атмосфере Глава XVIII. Физика атмосферы § 307. Атмосфера § 308. Тепловой баланс Земли § 309. Адиабатические процессы в атмосфере § 310. Облака § 311. Искусственные осадки § 312. Ветер § 313. Предсказание погоды Глава XIX. Тепловые машины § 314. Условия, необходимые для работы тепловых двигателей § 315. Паросиловая станция § 316. Паровой котел § 317. Паровая турбина § 318. Поршневая паровая машина § 319. Конденсатор § 320. Коэффициент полезного действия теплового двигателя § 321. Коэффициент полезного действия паросиловой станции § 322. Бензиновый двигатель внутреннего сгорания § 323. Коэффициент полезного действия двигателя внутреннего сгорания § 324. Двигатель Дизеля § 325. Реактивные двигатели § 326. Передача теплоты от холодного тела к горячему Ответы и решения к упражнениям Предметный указатель |
С. Элементарный учебник физики. Т.1. Механика. Теплота. Молекулярная физика. — М.: Наука, 1985. — 606 c.
Ограничение по высоте сифона
Хотя сифон использовался с древних времен, способы его эксплуатации вызывали споры 1,2,3,4,5,6 .
Были выдвинуты две конкурирующие модели: одна, в которой считается, что сифоны работают под действием силы тяжести и атмосферного давления, а другая, в которой используется гравитация и сцепление жидкости. Ключевым доказательством атмосферной модели является то, что максимальная высота сифона примерно равна высоте столба жидкости, который может поддерживаться атмосферным барометрическим давлением. В этой модели сифон считается двумя барометрами, расположенными «спина к спине». Еще одним доказательством в пользу атмосферной модели является тот факт, что сифонное течение может происходить с пузырьком воздуха внутри трубы, так что между молекулами воды нет физической связи. Доказательством в поддержку модели гравитационного сцепления является то, что сифоны, как было показано, работают в условиях вакуума 7,8,9 и модель может объяснить любопытную особенность, напоминающую водопад, когда сифон работает близко к барометрическому пределу 10 .
Обе модели сифона — атмосферная и когезионная — предсказывают, что максимальная высота сифона зависит от атмосферного атмосферного давления.
В случае атмосферной модели давление атмосферы требуется, чтобы удерживать столб воды вместе. В модели когезии предел объясняется тем, что давление в верхней части сифона падает ниже давления паров воды при данной температуре, так что возникает кавитация, т.е. вода начинает кипеть, разрывая столб.
Однако модель сцепления предсказывает, что если можно предотвратить кавитацию, то можно нарушить предел барометрической высоты. Причина сплоченности заключается в том, что поверхности требуют энергии, и поверхность вода/воздух ничем не отличается. Для воды поверхностную энергию часто называют поверхностным натяжением. Поверхностная энергия границы раздела вода/воздух составляет 0,072 Дж/м 2 . Создание пузырьков в воде требует энергии из-за энергии поверхности пузырьков. Чтобы пузырек был устойчивым, он должен поддерживаться либо внутренним давлением газа, либо эквивалентным напряжением (отрицательным давлением) в воде. Для газа в пузыре давление ( P ) определяется формулой (1).
Это уравнение 11 является точным для идеального газа, но является приближением для реального газа.
, где γ — поверхностная энергия (Дж/м 2 или Н/м), а r (м) — радиус пузырька. Хорошим контрольным давлением является атмосферное давление, которое составляет = 1,013 × 10 5 Па (Н/м 2 ). Внутреннее давление в одну атмосферу (или эквивалентное напряжение в воде) может поддерживать пузырек радиусом r , где:
То есть внутреннее давление в одну атмосферу создается пузырем радиусом 1,42 мкм (диаметром 2,8 мкм). Эквивалентно, для пустого пузыря диаметром 2,8 мкм возникло бы напряжение, равное выдержке в одну атмосферу. Пузырь меньшего размера будет поддерживать большее натяжение воды, а пузырь большего размера — меньшее натяжение воды. Пузырек диаметром 2,8 нм может выдержать давление воды, равное 1000 атмосфер (100 МПа).
Было проведено множество экспериментов по измерению прочности воды на разрыв 12,13,14,15,16,17,18,19,20 и были достигнуты значения до -150 МПа 21 .
Все эти эксперименты проводились на статических образцах. В этой статье мы впервые сообщаем о сифоне, работающем выше барометрического предела при окружающем атмосферном давлении. Таким образом, мы демонстрируем объемный поток воды под напряжением.
В начальном эксперименте 60 мл обычной водопроводной воды с 4 мл покрывающего слоя силиконового масла держали под вакуумом <10 −3 Па в течение периода более трех недель. Во время первоначального процесса дегазации значительные объемы газа были выделены как из воды, так и из покрывающих слоев. Этот процесс обычно связывают с кипением, но, как будет определено в последующих разделах, этот эффект полностью обусловлен растворенными газами, выходящими из воды. Небольшое количество воды (~2 мл) испарилось из начального объема, в основном за счет обнажения поверхности воды при прохождении крупных пузырьков через покрывающий слой.
После того, как вода и покрывающий слой были полностью дегазированы, дальнейшая потеря жидкости прекратилась.
После того, как судно на короткое время вернулось к атмосферному давлению, последующие откачки не привели к выделению большего количества газа из воды (видеоэпизод 1). Однако возврат контейнера к атмосферному давлению на несколько часов позволил реабсорбировать газ в покрывающий нефть слой и в течение более длительного периода в воду под ним. Этот газ снова высвобождался при повторном вакуумировании контейнера.
В следующем эксперименте когезионная прочность воды была проверена с использованием простой перевернутой U-образной трубки с основанием, находящимся в вакууме, наподобие барометра (рис. 1). Первоначально U-образная трубка была установлена ниже уровня поверхности жидкости, в то время как стеклянный сосуд был откачан, а все газы были полностью удалены сверху и внутри жидкости. Когда парциальное давление внутри сосуда снизилось до 7,5 ± 0,05 × 10 −1 Па, U-образную трубку подняли, подняв вершину трубки на высоту 300 мм над поверхностью масла. Предполагалось, что с плотностью немного меньшей, чем у воды, поверхность масла близка к гипотетической границе раздела вода-вакуум.
Было замечено, что вода образует непрерывный столб без пузырьков/полостей, образующихся в верхней части пробирки (рис. 2). Затем перевернутую U-образную трубку удерживали в этом положении более четырех недель. По истечении этого времени U-образную трубку наклонили еще больше, так что вершина оказалась на высоте 400 мм над поверхностью, при этом парциальное давление над жидкостью уменьшилось до 5 ± 0,05 × 10 −3 Па. В этом положении водяной столб был стабильным, а образование пузырьков в U-образной трубке не наблюдалось даже через несколько часов.
Верхнее изображение: Экспериментальная установка для дегазации воды; Изображение справа: увеличенный вид датчика Маклеода; Нижняя диаграмма: градуированный стеклянный мерный цилиндр объемом 100 мл, наполненный 60 мл воды и закрытый 5 мл масла, стоит на небольшом поддоне из плексигласа над турбомолекулярным насосом. Манометры имеют маркировку 1) APG-M-NW16, 2) AIM-S-NW25 и McLeod.
Изображение в полный размер
Рисунок 2Схема барометра с U-образной трубкой, заполненного водой.
На нижнем рисунке показано положение во время вакуумирования и дегазации воды с помощью маслозащитного слоя, а на верхнем рисунке показано положение U-образной трубки в наклонном положении, когда основание удерживается в вакууме.
Изображение в полный размер
Для проверки способности воды сохранять когезию в условиях потока был сконструирован стеклянный сифон таким образом, чтобы оба резервуара могли находиться в условиях высокого вакуума (рис. 3), аналогично тому, как это делалось ранее. от Ноукса 8 . При такой схеме в процессе дегазации с U-образной трубкой, установленной ниже уровня масла, уровень жидкости в обоих резервуарах был одинаковым при заполнении каждого наполовину. Когда U-образная трубка затем была поднята в вертикальное положение, смещение в положении позволило одному резервуару подняться дальше, чем другому, что привело к небольшой разнице в высоте.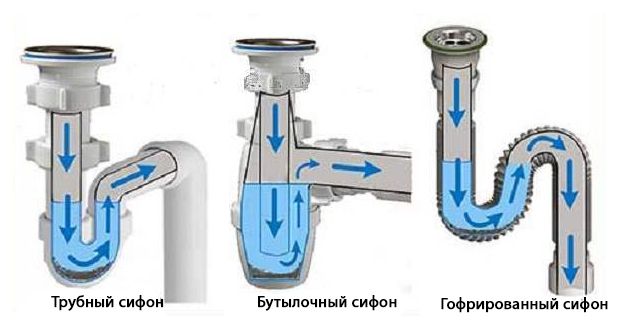
Когда U-образная трубка изначально находилась в нижнем положении, вода дегазировалась до парциального давления 9,5 ± 0,05 × 10 −1 Па. камера в нижнюю через сифонную трубку в нижнюю камеру (видеоэпизод 2).
Фотография U-образного барометра в вакууме.
Показания давления указаны в Па, а высота вершины составляет 300 мм над поверхностью жидкости.
Изображение полного размера
В то время как поток инициировался независимо от атмосферного давления внутри сифона, было отмечено, что движение резервуаров между статическими и проточными условиями обнажает поверхности, которые ранее были покрыты водой. При этом наблюдалось повышение давления в области вакуума выше 10 3 Па. Понимая, что это представляет собой фундаментальный недостаток, в этой и в предыдущих попытках других создать водяной сифон в условиях вакуума было сочтено, что сифон средней длины не может окончательно исключить влияние давления пара на поддержание столбец.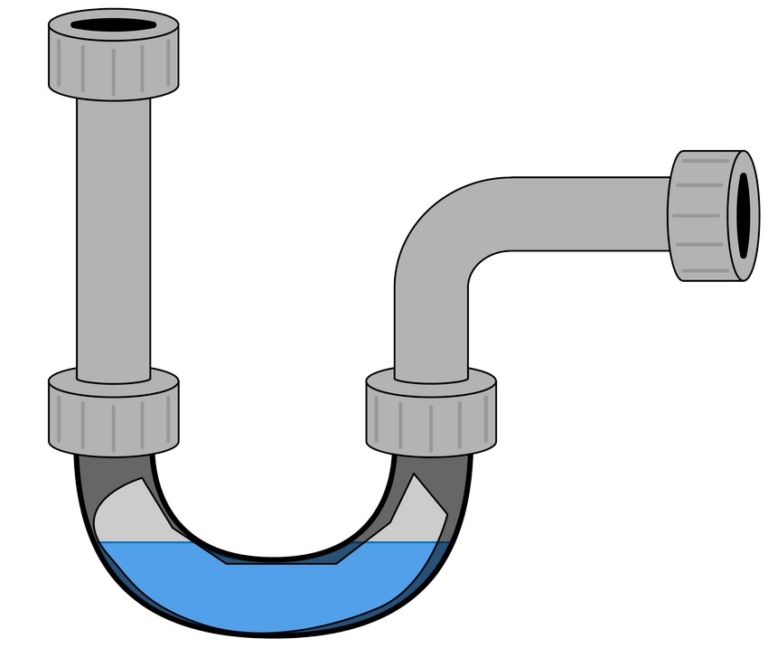
Для снижения влияния внешнего давления, действующего на столб жидкости, был сконструирован второй сифон, работающий в атмосферных условиях, высотой выше номинального барометрического предела 10 м, с использованием воды, дегазированной с помощью вакуум-эксикатора (рис. 4).
Рисунок 4Схема водяного сифона под вакуумом.
На нижнем рисунке показано положение при вакуумировании и дегазации воды с масляным покрывающим слоем, а на верхнем рисунке показано положение сифона под наклоном при перетекании жидкости из верхнего в нижний резервуар, при этом каждый резервуар находится под вакуумом.
Изображение в полный размер
Высота сифона, определяемая как расстояние по вертикали между поверхностью воды в верхнем резервуаре и вершиной трубы, начиная с 1498 ± 2 см и увеличилась до 1504 ± 2 см (рис. 5). Барометрическое давление во время эксперимента составляло 99,8 ± 0,1 кПа. Эксперимент повторялся несколько раз, и пример показан в соответствующем дополнительном видео (видеоэпизод 3).
После открытия обоих кранов в основании предварительно залитого сифона вода вытекала только из нижней из двух ножек сифона (видеоэпизод 4). Приблизительно 400 мл воды перетекло из верхнего в нижний резервуар за 850 с, что соответствует расходу 4,7 ± 0,05 × 10 −7 м 3 с −1 и средней скоростью 1,7 ± 0,05 × 10 −2 м с −1 .
Схема сифона выше барометрического предела с резервуарами, открытыми для воздуха.
Вода в верхнем резервуаре покрыта 5 мм слоем силиконового масла. Шкив используется на вершине для поддержки длины трубы и предотвращения перегибов в трубе.
Изображение в полный размер
Для измерения влияния капиллярного действия на подъем воды в сифонной трубке один конец пустой сифонной трубки был погружен в дегазированную воду, которая была открыта для воздуха, а другой конец открытый конец трубки удерживали над уровнем жидкости. Поскольку разницы между высотой жидкости внутри нейлоновой трубки и снаружи не наблюдалось, капиллярное действие не принималось во внимание как играющее какую-либо существенную роль в сифонном процессе.
Возможность полной дегазации воды всегда представляла собой серьезную проблему при проведении экспериментов по изучению прочности жидкости на растяжение. Широко известно, что большие различия, наблюдаемые как внутри, так и между различными методами исследования свойств воды, обусловлены непредсказуемой природой газов, растворенных в 22 . В воде, свободной от всех растворенных газов, пузырьки образуются только тогда, когда энергия, полученная при образовании полости, превышает энергию связи окружающих молекул.
Таким образом, образование полостей в полностью дегазированной воде представляет собой предел сцепления молекул воды. Из используемых методов, таких как кипячение, обработка ультразвуком, мембранная дегазация и оттаивание замораживающим насосом, те, при которых вода подвергается воздействию вакуума, обычно считаются наиболее эффективными для удаления всех растворенных газов. Это можно понять, экстраполируя до предела закон Генри
, где C — растворимость газа при фиксированной температуре в определенном растворителе, k — постоянная Генри, а P gas — парциальное давление газа над жидкостью.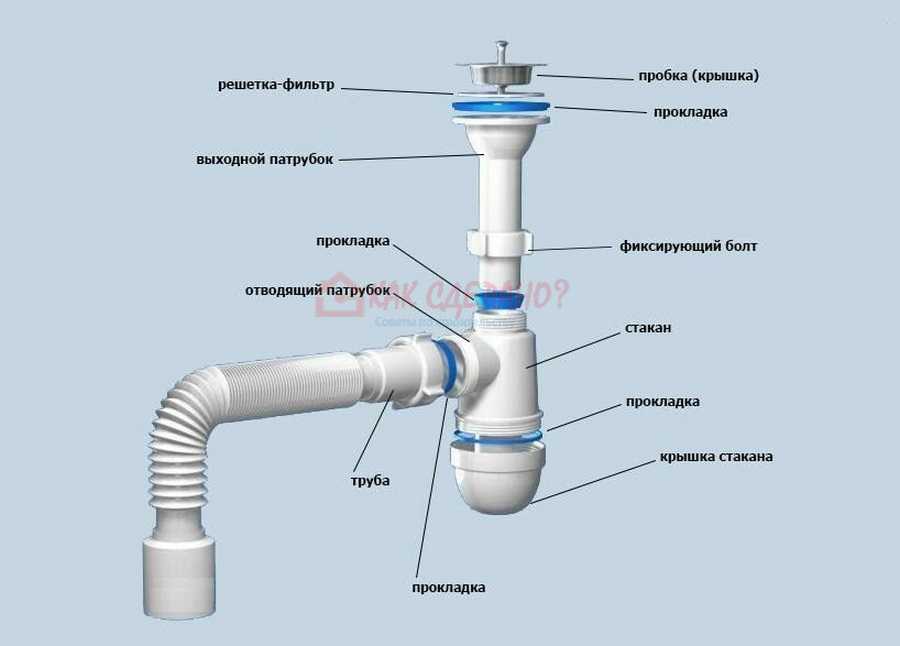
Соответственно, при нулевом давлении количество растворенного газа также должно быть равным нулю. Однако из-за практических ограничений трудно достичь давления над поверхностью намного ниже давления пара, которое для воды при 20 °C составляет приблизительно 2,33 кПа, и, следовательно, всегда будет присутствовать некоторое количество растворенных газов.
При температурах выше точки замерзания и ниже точки кипения связи между соседними молекулами воды на границе раздела жидкость-воздух постоянно разрушаются и восстанавливаются. Этот постоянный обмен между уходящим и вновь соединяющимся молекулами обычно находится в равновесии при атмосферном давлении и комнатной температуре, вот почему мы так много видим жидкой воды на Земле. Однако, как только давление над границей раздела уменьшается или температура жидкости ниже повышается, равновесие смещается, и молекулы воды в среднем теряются из объема жидкости.
Простой метод преодоления потери воды заключается в изменении энергетического барьера на поверхности воды путем нанесения на поверхность слоя несмешиваемой жидкости.
При плавании жидкости с низким удельным весом и сверхнизким давлением пара над водой молекулы на границе раздела не могут покинуть воду и мигрировать через покрывающую жидкость на поверхность. Таким образом, потери на испарение, которые обычно происходят ниже давления водяного пара, значительно уменьшаются, если не полностью сводятся на нет.
После первоначальной дегазации воды не было дальнейших потерь на испарение или кавитации в объемной жидкости или на любой поверхности раздела, когда давление окружающей среды было ниже 10 −3 Па. сила, действующая на воду, поднимающая давление выше точки парения, с покрывающим слоем всего 5 мм, масло будет способствовать нисходящему давлению менее 43 Па. маслом на стадии дегазации было только падение температуры, измеренное ртутным термометром, когда поверхность воды подвергалась воздействию вакуума, как это происходило, когда на поверхности взрывались большие пузыри. Затем температура воды со временем постепенно повышалась, возвращаясь к температуре окружающей среды в лаборатории.
Это очень медленное повышение температуры было частично связано с некоторой лучистой энергией через переднюю часть камеры из плексигласа, но преимущественно с теплопроводностью через устройство. Наблюдалось, что в течение 3 недель в условиях вакуума температура воды оставалась стабильной на уровне примерно 21 °C.
Это удивительное поведение объясняется динамикой испарения, когда в среднем наиболее энергичные молекулы стремятся покинуть поверхность первыми. В этом случае за счет увеличения энергетического барьера на поверхности испарение не может происходить, поэтому чистая потеря энергии системой незначительна или отсутствует, оставляя температуру постоянной. Следовательно, хотя масло действует как эффективный барьер для испарения воды, оно не препятствует переносу газа в любом направлении и не изменяет значительно градиент давления внутри жидкости. Следовательно, эти эксперименты показывают, что в то время как открытая вода действительно испаряется при низких парциальных давлениях, как и следовало ожидать, внутренняя кавитация или зародышевое кипение не возникают при комнатной температуре даже при чрезвычайно низких давлениях окружающей среды.
For a siphon with dissolved gases the maximum height ( h m ) of a siphon is
where P 0 is the ambient atmospheric pressure, P v — давление паров воды, v — средняя скорость воды, а другие символы определены ранее в этой статье. Выражение для атмосферной модели такое же, как уравнение (3), за исключением отсутствия P v срок.
Сифон в эксперименте, описанном в этой статье, явно работал выше барометрического предела, который при заданном барометрическом давлении составлял 10,18 ± 0,01 м для атмосферной модели и 9,94 ± 0,01 м для модели сцепления (без учета пренебрежимо малого члена скорости ). Таким образом, очевидно, что атмосферное давление не играет никакой роли в переносе воды через вершину сифонной трубки. Поэтому ясно, что для ситуаций, когда кавитации не возникает, требуется новое уравнение для максимальной высоты сифона.
Новое уравнение намного проще и имеет вид
, где TS w — предел прочности воды на разрыв. Так, например, если предел прочности на растяжение образца воды составляет 1 МПа, максимальная высота сифона будет около 100 м. В случае с сифоном в этом эксперименте можно сказать, что предел прочности воды на разрыв был больше -0,15 МПа.
Экстраполируя эти результаты даже самых консервативных экспериментальных измерений напряжения, при котором возникает кавитация, становится возможным, что когезионная прочность полностью дегазированной воды способна поддерживать непрерывный вертикальный столб высотой более нескольких сотен метров. Хотя проведенный здесь эксперимент и близко не достиг предсказанного абсолютного предела, он проливает свет на устойчивость текущей воды под действием растягивающего напряжения и на возможность создания аппарата подходящих размеров для проверки такого предела. Эти эксперименты также поддерживают теорию сцепления и натяжения сокодвижения деревьев.
Было бы интересно провести дальнейшие эксперименты, чтобы увидеть, можно ли использовать проточный сифон на высоте более 100 м. Если в вершине сифона можно поддерживать напряжения, достигающие переходного напряжения в несколько сотен бар, то, в принципе, сифон должен работать до высоты в несколько километров. Однако было бы сложно проверить это экспериментально, поскольку требуется вертолет или БПЛА с потолком в несколько километров, способный выдержать несколько кг заполненных водой труб и кабеля, поддерживающего сифон. Также было бы интересно повторить эксперимент с трубой большего диаметра. Ввиду множества аномалий объемной воды 23 , было бы интересно изучить физические свойства воды в режиме отрицательного давления сифона выше 10 м.
Что такое сифон? — Pump & Flow
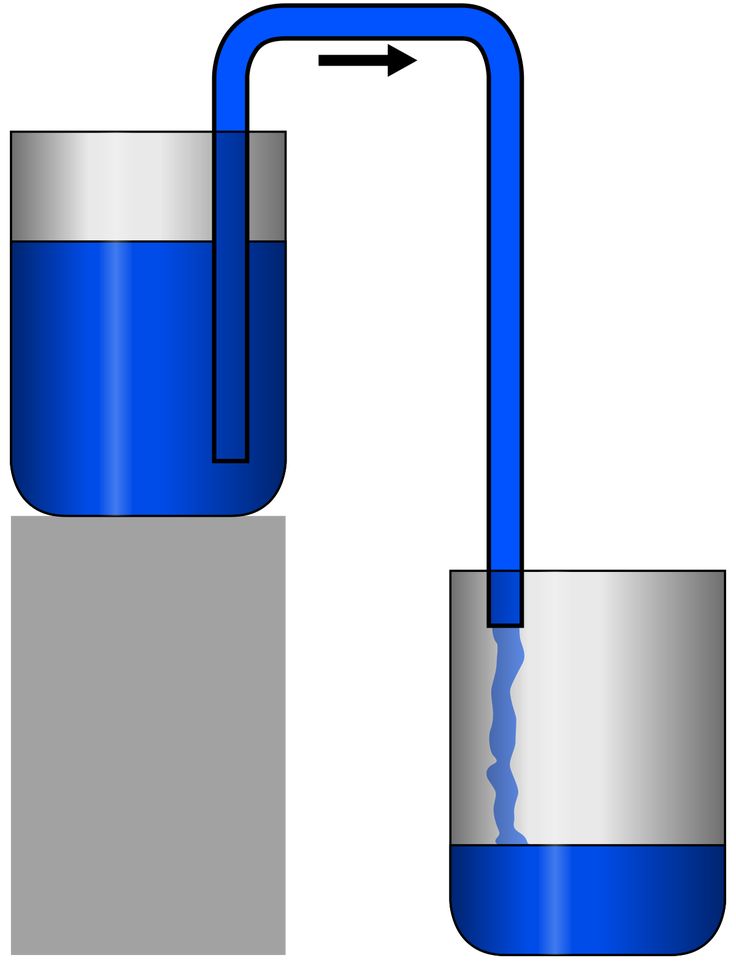
Сифон – это любое устройство (обычно труба в форме перевернутой U ), используемое для перекачки жидкости с большей высоты на меньшую без использования насосов.
Как это работает?
Сифоны сначала транспортируют жидкость вверх через более короткую часть трубы – обычно с помощью внешнего насоса или всасывания (ЗАПРАВКА) – затем используют силу гравитации жидкости, падающей через более длинную нижнюю часть трубы, и атмосферное давление для поддерживать поток жидкости даже при снятии силы заливки.
это
, известный как эффект сифона.
Кто изобрел?
Люди веками использовали сифоны для самых разных целей. Самые ранние появления сифонов встречаются в древнеегипетском искусстве. На нем изображены они, использующие сифоны для извлечения вина из больших кувшинов для хранения. Они изобретательно использовали сифоны, чтобы отделить вино от поверхностных примесей и примесей на дне.
Греческий математик Герой Александрийский первым описал эффект сифона. Он провел множество опытов и написал об этом в своем инженерном трактате Пневматический .
Как они используются сегодня?
Сегодня сифоны имеют широкий спектр применения благодаря низкому энергопотреблению и простой конструкции. Они обычно используются в бытовых целях, таких как туалеты, пивные краны и простые садовые разбрызгиватели.
Сифоны также широко используются для орошения сельскохозяйственных угодий. Из-за низкого энергопотребления и стоимости они очень подходят для транспортировки воды на большие расстояния от источников воды до плодородных засушливых долин.
Отличные примеры ирригационных проектов с сифонным приводом можно найти на плантациях сахарного тростника на Гавайях, США, и на хлопковых полях в Квинсленде, Австралия.
Какая наука стоит за эффектом высасывания?
Было выдвинуто множество теорий, объясняющих работу сифонов. До сих пор ведутся активные споры о том, что на самом деле отвечает за эффект перекачивания. Но ученые пришли к выводу, что это результат двух факторов. Атмосферное давление и теория цепей.
Теория атмосферного давления была одной из первых теорий, сформулированных для описания эффекта сифонирования. Он предполагает, что когда жидкость всасывается через трубку, акт всасывания вызывает перепад давления в трубке с образованием области низкого давления в самой высокой точке. Этот перепад давления заставляет жидкость течь от
области высокого давления на поверхности пласта к области низкого давления в самой высокой точке. Главный недостаток этой теории заключается в том, что сифоны продемонстрировали работу в условиях высокого вакуума (без воздуха, без атмосферного давления).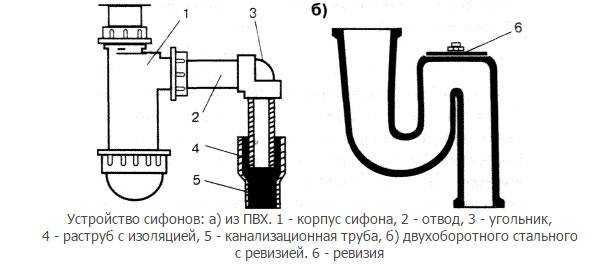
Более поздняя теория состоит в том, что гравитация и сцепление работают вместе. Он основан на цепной модели. Эта модель рассматривает жидкость как цепочку, связанную когезионными связями. Цепь сначала тянется вверх через трубку под действием другой силы, пока не пройдет изгиб, затем вступает в действие сила тяжести, тянущая всю жидкость вниз, как цепь по шкиву, пока резервуар не опустеет. Эта теория также была отвергнута, потому что сифоны были сделаны для жидкостей с низкими или слабыми силами сцепления.
Сегодня инженеры используют комбинацию обеих теорий для объяснения эффекта сифонирования в различных условиях.
Наиболее популярным математическим приближением, используемым для моделирования жидкостей в сифонах, является теория Бернулли.
Математически это выражается следующим образом:
Где v=локальная скорость, g=ускорение свободного падения, P=давление, y=вертикальное расстояние от поверхности резервуара, ρ=плотность жидкости
Это уравнение моделирует весь сифон как система.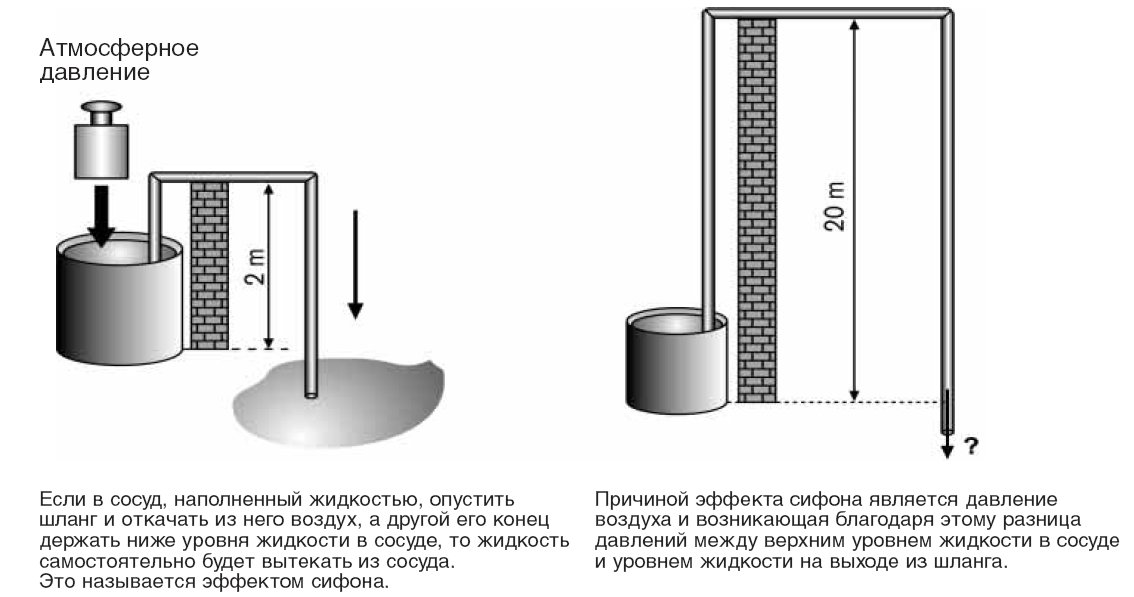
Допустим, у нас есть погружной насос в резервуаре высотой RL +5м. Вода откачивается через стену RL +8 м и сбрасывается при RL 0 м. Найдем скорость истечения на выходе при использовании трубки в качестве сифона.
Чтобы найти это, применим уравнение Бернулли к трем точкам в системе:
1. Поверхность резервуара
2. Самая высокая точка
3. Точка нагнетания
Предположим, что насос используется для заполнения сифона и отключается после начала потока, а потери на трение и другие эффекты пренебрежимо малы.
На поверхности(2):
Скорость V с = 0 м/с (Мы моделируем поверхность резервуара как бесконечную)
Давление P с = P atm (атмосферное давление)
Расстояние от поверхность (y) = 0 м
В высшей точке (h(3)):
В точке h скорость = V ч
Давление = P ч > P атм
В нижней точке (точка нагнетания d(4)):
Скорость V d = V ч (Поскольку они находятся на одной линии потока)
Давление =P ч атм
Расстояние от поверхности = 0-5= -5м
Чтобы найти скорость V d мы приравниваем (2) к (4), что дает нам:.
Переставляя имеем:
Подставляя значения и решая, получаем скорость разряда 90,9 м/с
Однако существует предел условий, при которых сифон может поддерживаться. Основным ограничением для поддержания сифона является воздух. Сифон должен быть герметичным, потому что большое количество воздуха в системе может нарушить вакуум, от которого зависит работа сифона.
Также высота сифона ограничена давлением паров жидкости и местным атмосферным давлением. Например, для поддержания сифона в системе откачки воды из резервуара на уровне моря расстояние между поверхностью резервуара и самая высокая точка трубы не должна быть выше 10 м.
Когда самая высокая точка трубы находится на высоте более 10 м, давление в самой высокой точке трубы становится равным давлению водяного пара. Когда это происходит, вода начинает кипеть, разрушая силы сцепления, удерживающие цепочку жидкости вместе, тем самым разрывая сифон. Интересно, однако, что для дегазированной воды были сконструированы сифоны гораздо большей высоты.
Как трение влияет на сифонирование?
В сифонах сила трения на входе, выходе и внутренних стенках трубок и сила инерции воды часто препятствуют потоку при заполнении сифонной трубки. Но это обычно преодолевается силой заливки (накачки), потому что в большинстве практических применений трубка обычно заполняется внешней силой до начала сифонирования.
Когда поток начался и питается только сифоном, потеря напора на трение становится функцией скорости потока, обеспечиваемой сифоном. Потери напора на трение увеличиваются с увеличением скорости потока, т. е. по мере того, как поток становится более турбулентным, потери на трение увеличиваются.
Поскольку потери от трения являются функцией скорости потока, они не останавливают поток, а только уменьшают скорость потока.
Чтобы найти падение скорости от трения, мы вводим в уравнение коэффициент сопротивления K для учета потерь от трения.
K = (f *L /D) + 1,9 (Другие источники)……….(6)
Где: f = коэффициент трения трубы (железо = 0,019, сталь = 0,013, пластик = . 007)
L = изменение точек станции (длина пробега), (м)
d = внутренний диаметр трубы (м)
Таким образом, модифицируя (5), мы получаем скорость потока (м/с):
Как сифонирование влияет на насосные системы?
Как мы видели в предыдущих разделах, эффект сифона имеет множество применений в области сельского хозяйства, машиностроения и простых повседневных приложений. Но это также может стать проблемой в некоторых системах.
В некоторых насосных системах сифонный эффект может использоваться в сочетании с определенными конфигурациями труб для увеличения напора, но он также может вызвать определенные проблемы, если он не спроектирован должным образом.
Как это может произойти в насосных системах?
Сифонирование может произойти в насосной системе из-за конфигурации труб. Сифоны управляются вертикальным расстоянием между резервуаром и точкой слива. Это происходит в ситуациях, когда точка нагнетания находится на уровне ниже водохранилища или точки откачки.
Скорость потока, полученная в сифоне, и объемный расход определяются расстоянием по вертикали между точкой накачки и точкой нагнетания. Чем больше расстояние, тем больше скорость потока.
Какие проблемы может вызвать сифонирование?
Возьмем погружной насос из приведенного выше примера. Предположим, что насос должен был наполнять бассейн и выключаться после достижения определенного уровня, из-за расположения резервуара и точки слива вода будет продолжать течь даже после выключения насоса, вызывающего бассейн. переполниться.
Другая проблема возникает, если мы поменяем конфигурацию на противоположную, допустим, насос перекачивает воду из нижнего резервуара в верхний «бассейн».
После выключения насоса перепад давления нетто, перемещающий воду из нижней части в верхнюю, и сточные воды из бассейна начинают течь обратно в резервуар. Это известно как обратное сифонирование и представляет собой серьезную проблему для общественного здравоохранения, поскольку опасные загрязнители могут попасть в систему водоснабжения.
Как мы можем решить эти проблемы?
Существуют различные методы проектирования для решения этих проблем, наиболее распространенные из которых часто включают размещение клапанов на одной линии с потоком. Вот некоторые примеры таких клапанов:
Электромагнитный клапан: Это клапан с электрическим управлением, который помогает предотвратить перелив, перекрывая поток воды в трубе сразу после остановки насоса.
Обратный клапан: Этот клапан также можно использовать для предотвращения обратного сифонирования, когда он расположен на одной линии с потоком. Его специальная конфигурация помогает обеспечить поток только в одном направлении.
Обычно его ставят сразу после насоса, чтобы защитить его от обратного потока.
Но в некоторых случаях электромагнитный клапан/обратный клапан может быть либо слишком дорогим, либо не совсем подходящим по конструкции.
В этом случае используется комбинированный клапан прерывателя воздуха/вакуума. Воздушно-вакуумный клапан обычно устанавливается в самой высокой точке системы. Он выполняет двойную функцию: удаляет лишний воздух из системы, чтобы предотвратить повышение давления, и впускает воздух в систему, чтобы нарушить вакуум и свести на нет эффект сифона.
Для сложных трубопроводов протяженностью сотни метров необходимо установить клапаны различных форм и размеров в разных точках по длине трубы, чтобы обеспечить надлежащую вентиляцию. Но для простой конструкции, подобной приведенной выше, можно использовать простой вакуумный прерыватель. Он должен быть установлен в самой высокой точке и должен использоваться соответствующий размер.
Как подобрать размер воздушного/вакуумного клапана:
При выборе размера воздушного/вакуумного выпускного клапана большинство инженеров используют стандартное эмпирическое правило: 25 мм диаметра клапана на 0,3 м диаметра трубы.