Если на первичную обмотку ненагруженного трансформатора подать напряжение: Задача по физке — 12096

Элементарный учебник физики Т2

Элементарный учебник физики Т2

Ландсберг Г.С. Элементарный учебник физики. Т.2. Электричество и магнетизм. — М.: Наука, 1985. — 479 c. Один из лучших курсов элементарной физики, завоевавший огромную популярность. Достоинством курса является глубина изложения физической стороны рассматриваемых процессов и явлений в природе и технике. В новом издании структура курса осталась прежней, однако в изложении проведена система единиц СИ, терминология и обозначения единиц физических величин приведены в соответствие с действующим ГОСТ. Для слушателей и преподавателей подготовительных отделений и курсов вузов, старшеклассников общеобразовательных и профессиональных школ, а также лиц, занимающихся самообразованием и готовящихся к поступлению в вуз. Оглавление ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ Глава I. Электрические заряды § 1. Электрическое взаимодействие. § 2. Проводники и диэлектрики. § 3. Разделение тел на проводники и диэлектрики § 4. Положительные и отрицательные заряды § 5. Что происходит при электризации? § 6. Электронная теория. § 7. Электризация трением. § 8. Электризация через влияние. § 9. Электризация под действием света. § 10. Закон Кулона. § 11. Единица заряда. Глава II. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ § 12. Действие электрического заряда на окружающие тела. § 13. Понятие об электрическом поле. § 14. Напряженность электрического поля. § 15. Сложение полей. § 16. Электрическое поле в диэлектриках и в проводниках. § 17. Графическое изображение полей. § 18. Основные особенности электрических карт. § 19. Применение метода линий поля к задачам электростатики. § 20. Работа при перемещении заряда в электрическом поле. § 21. Разность потенциалов (электрическое напряжение). § 22. Эквипотенциальные поверхности. § 23. В чем смысл введения разности потенциалов? § 24. Условия равновесия зарядов в проводниках. § 25. Электрометр. § 26. В чем различие между электрометром и электроскопом? § 27. Соединение с Землей. § 28. Измерение разности потенциалов в воздухе. Электрический зонд. § 29. Электрическое поле Земли. § 30. Простейшие электрические поля. § 31. Распределение зарядов в проводнике. Клетка Фарадея. § 32. Поверхностная плотность заряда. § 33. Конденсаторы. § 34. Различные типы конденсаторов. § 35. Параллельное и последовательное соединение конденсаторов. § 36. Диэлектрическая проницаемость. § 37. Почему электрическое поле ослабляется внутри диэлектрика? § 38. Энергия заряженных тел. Энергия электрического поля. Глава III. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК § 39. Электрический ток и электродвижущая сила. § 40. Признаки электрического тока. § 41. Направление тока. § 42. Сила тока. § 43. «Скорость электрического тока» и скорость движения носителей заряда. § 44. Гальванометр. § 45. Распределение напряжения в проводнике с током. § 46. Закон Ома. § 47. Сопротивление проводов. § 48. Зависимость сопротивления от температуры. § 49. Сверхпроводимость. § 50. Последовательное и параллельное соединение проводников. § 51. Реостаты. § 52. Распределение напряжения в цепи. § 53. Вольтметр. § 54. Каким должно быть сопротивление вольтметра и амперметра? § 55. Шунтирование измерительных приборов. Глава IV. ТЕПЛОВОЕ ДЕЙСТВИЕ ТОКА § 56. Нагревание током. Закон Джоуля-Ленца. § 57. Работа, совершаемая электрическим током. § 58. Мощность электрического тока. § 59. Контактная сварка. § 60. Электрические нагревательные приборы. Электрические печи. § 61. Понятие о расчете нагревательных приборов. § 62. Лампы накаливания. § 63. Короткое замыкание. § 64. Электрическая проводка. Глава V. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ЭЛЕКТРОЛИТЫ § 65. Первый закон Фарадея. § 66. Второй закон Фарадея. § 67. Ионная проводимость электролитов. § 68. Движение ионов в электролитах. § 69. Элементарный электрический заряд. § 70. Первичные и вторичные процессы при электролизе. § 71. Электролитическая диссоциация. § 72. Градуировка амперметров при помощи электролиза. § 73. Технические применения электролиза. Глава VI. ХИМИЧЕСКИЕ И ТЕПЛОВЫЕ ГЕНЕРАТОРЫ ТОКА § 74. Введение. Открытие Вольты. § 75. Правило Вольты. Гальванический элемент. § 76. Как возникают э. д. с. и ток в гальваническом элементе? § 77. Поляризация электродов. § 78. Деполяризация в гальванических элементах. § 79. Аккумуляторы. § 80. Закон Ома для замкнутой цепи. § 81. Напряжение на зажимах источника тока и э. д. с. § 82. Соединение источников тока. § 83. Термоэлементы. § 84. Термоэлементы в качестве генераторов. § 85. Измерение температуры с помощью термоэлементов. Глава VII. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ МЕТАЛЛЫ § 86. Электронная проводимость металлов. § 87. Строение металлов. § 88. Причина электрического сопротивления. § 89. Работа выхода. § 90. Испускание электронов накаленными телами. Глава VIII. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ГАЗЫ § 91. Самостоятельная и несамостоятельная проводимость газов. § 92. Несамостоятельная проводимость газа. § 93. Искровой разряд. § 94. Молния. § 95. Коронный разряд. § 96. Применения коронного разряда. § 97. Громоотвод. § 98. Электрическая дуга. § 99. Применения дугового разряда. § 100. Тлеющий разряд. § 101. Что происходит при тлеющем разряде? § 102. Катодные лучи. § 103. Природа катодных лучей. § 104. Каналовые лучи. § 105. Электронная проводимость в высоком вакууме. § 106. Электронные лампы. § 107. Электроннолучевая трубка. Глава IX. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ПОЛУПРОВОДНИКИ § 108. Природа электрического тока в полупроводниках. § 109. Движение электронов в полупроводниках. § 110. Полупроводниковые выпрямители. § 111. Полупроводниковые фотоэлементы. Глава X. ОСНОВНЫЕ МАГНИТНЫЕ ЯВЛЕНИЯ § 112. Естественные и искусственные магниты. § 113. Полюсы магнита и его нейтральная зона. § 114. Магнитное действие электрического тока. § 115. Магнитные действия токов и постоянных магнитов. § 116. Происхождение магнитного поля постоянных магнитов. § 117. Гипотеза Ампера об элементарных электрических токах. Глава XI. МАГНИТНОЕ ПОЛЕ § 118. Магнитное поле и его проявления. Магнитная индукция. § 119. Магнитный момент. Единица магнитной индукции. § 120. Измерение магнитной индукции поля с помощью магнитной стрелки. § 121. Сложение магнитных полей. § 122. Линии магнитного поля. § 123. Приборы для измерения магнитной индукции. Глава XII. МАГНИТНЫЕ ПОЛЯ ЭЛЕКТРИЧЕСКИХ ТОКОВ § 124. Магнитное поле прямолинейного проводника и кругового витка с током. § 125. Магнитное поле соленоида. Эквивалентность соленоида и полосового магнита. § 126. Магнитное поле внутри соленоида. Напряженность магнитного поля. § 127. Магнитное поле движущихся зарядов. Глава XIII. МАГНИТНОЕ ПОЛЕ ЗЕМЛИ § 128. Магнитное поле Земли. § 129. Элементы земного магнетизма. § 130. Магнитные аномалии и магнитная разведка полезных ископаемых. § 131. Изменение элементов земного магнетизма с течением времени. Магнитные бури. Глава XIV. СИЛЫ, ДЕЙСТВУЮЩИЕ В МАГНИТНОМ ПОЛЕ НА ПРОВОДНИКИ С ТОКОМ § 132. Введение. § 133. Действие магнитного поля на прямолинейный проводник с током. Правило левой руки. § 134. Действие магнитного поля на виток или соленоид с током. § 135. Гальванометр, основанный на взаимодействии магнитного поля и тока. § 136. Сила Лоренца. § 137. Сила Лоренца и полярные сияния. Глава XV. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ § 138. Условия возникновения индукционного тока. § 139. Направление индукционного тока. Правило Ленца. § 140. Основной закон электромагнитной индукции. § 141. Электродвижущая сила индукции. § 142. Электромагнитная индукция и сила Лоренца. § 143. Индукционные токи в массивных проводниках. Токи Фуко. Глава XVI. МАГНИТНЫЕ СВОЙСТВА ТЕЛ § 144. Магнитная проницаемость железа. § 145. Магнитная проницаемость различных веществ. Вещества парамагнитные и диамагнитные. § 146. Движение парамагнитных и диамагнитных тел в магнитном поле. Опыты Фарадея. § 147. Молекулярная теория магнетизма. § 148. Магнитная защита. § 149. Особенности ферромагнитных тел. § 150. Основы теории ферромагнетизма. Глава XVII. ПЕРЕМЕННЫЙ ТОК § 151. Постоянная и переменная электродвижущая сила. § 152. Опытное исследование формы переменного тока. Осциллограф. § 153. Амплитуда, частота и фаза синусоидального переменного тока и напряжения. § 154. Сила переменного тока. § 155. Амперметры и вольтметры переменного тока. § 156. Самоиндукция. § 157. Индуктивность катушки. § 158. Прохождение переменного тока через конденсатор и катушку с большой индуктивностью. § 159. Закон Ома для переменного тока. Емкостное и индуктивное сопротивления. § 160. Сложение токов при параллельном включении сопротивлений в цепь переменного тока. § 161. Сложение напряжений при последовательном соединении сопротивлений в цепи переменного тока. § 162. Сдвиг фаз между током и напряжением. § 163. Мощность переменного тока. § 164. Трансформаторы. § 165. Централизованное производство и распределение электрической энергии. § 166. Выпрямление переменного тока. Глава XVIII. ЭЛЕКТРИЧЕСКИЕ МАШИНЫ: ГЕНЕРАТОРЫ, ДВИГАТЕЛИ, ЭЛЕКТРОМАГНИТЫ § 167. Генераторы переменного тока. § 168. Генераторы постоянного тока. § 169. Генераторы с независимым возбуждением и с самовозбуждением. § 170. Трехфазный ток. § 171. Трехфазный электродвигатель. § 172. Электродвигатели постоянного тока. § 173. Основные рабочие характеристики и особенности двигателей постоянного тока с параллельным и последовательным возбуждением. § 174. Коэффициент полезного действия генератора и двигателя. § 175. Обратимость электрических генераторов постоянного тока. § 176. Электромагниты. § 177. Применение электромагнитов. § 178. Реле и их применения в технике и автоматике. Ответы и решения к упражнениям Приложения Предметный указатель Таблицы

Задачи на тему «Трансформатор» с решением

Трансформатор – устройство для изменения напряжения или тока. В сегодняшней статье рассмотрим несколько простых задач на расчет трансформаторов.

Подписывайтесь на нас в телеграме, чтобы не пропустить ничего важного. А если хотите получить скидку – загляните на наш второй канал с акциями и бонусами для клиентов.

Задачи на расчет трансформаторов

Специально для тех, кто не знает, как подступиться к задачам по физике, мы подготовили памятку и собрали вместе более 40 формул по разным темам.

Задача на трансформатор №1

Условие

Определите напряжение на концах первичной обмотки трансформатора,имеющей N1=2000 витков, если напряжение на концах вторичной обмотки, содержащей N2=5000 витков, равно 50 В. Активными сопротивлениями обмоток трансформатора можно пренебречь.

Решение

Применим форулу для коэффициента трансформации:

k=N1N2=U1U2

Из данной формулы следует, что:

U1=U2·N1N2

Подставим значения и вычислим:

U1=50·20005000=20 В

Ответ: 20 В.

Задача на трансформатор №2

Условие

Первичная обмотка трансформатора находится под напряжением 220 В, по ней проходит ток 0,5 А. На вторичной обмотке напряжение составляет 9,5 В, а сила тока равна 11 А. Определите коэффициент полезного действия трансформатора.

Решение

Формула для коэффициента полезного действия трансформатора:

η=P2P1·100%

Здесь P=UI –  мощность тока в обмотке.

Возьмем данные из условия и применим указанную формулу:

η=U2I2U1I1·100%η=9,5·11220·0,5·100%=95%

Ответ: 95%

Задача на трансформатор №3

Условие

Напряжение на первичной обмотке понижающего трансформатора 220 В, мощность 44 Вт. Определите силу тока во вторичной обмотке, если отношения числа витков обмоток равно 5. Потерями энергии можно пренебречь

Решение

Напряжение на вторичной обмотке будет равно:

U2=U1kU2=2205=44 В

Если считать, что потерь энергии нет, то мощность во вторичной обмотке будет такая же, как и в первичной:

I2=P2U2=44 Вт44 В=1 А

Ответ: 1А

При решении задач не забывайте проверять размерности величин!

Задача на трансформатор №4

Условие

Понижающий трансформатор включен в сеть с напряжением 1000 В и потребляет от сети мощность, равную 400 Вт. Каков КПД трансформатора, если во вторичной обмотке течет ток 3,8 А, а коэффициент трансформации равен 10?

Решение

Сначала определим напряжение на вторичной обмотке трансформатора:

U2=U1k=100010=100 В

Запишем формулу для КПД трансформатора и рассчитаем:

η=P2P1·100%=U2I2P1·100%η=100·3,8400·100%=95%

Ответ: 95%

Задача на трансформатор №5

Условие

Вторичная обмотка трансформатора, имеющая 95 витков, пронизывается магнитным потоком, изменяющимся со временем через один виток по закону Ф=0,01sin100πt.  Напишите формулу, выражающую зависимость ЭДС во вторичной обмотке от времени.

Решение

По закону электромагнитной индукции:

ε=-NdФdt

Продифференцируем магнитный поток по времени:

dФdt=d(0,01sin100πt)dt=0,01·100π·cos100πt=πcos100πt

Подставим результат в формулу для ЭДС:

ε=-Nπcos(100πt)

От минуса в данном выражении можно избавиться с помощью формул тригонометрии. Сделаем это и запишем окончательный результат:

ε=Nπsin(100πt-π2)=95πsin(100πt-π2)

Ответ: 95πsin(100πt-π2)

Вопросы на тему «Трансформаторы»

Вопрос 1. Что такое трансформатор?

Ответ. Трансформатор – статическое устройство, имеющее две или более связанные обмотки на магнитопроводе. Трансформатор предназначен для преобразования одной величины напряжения и тока в другое без изменения частоты посредством электромагнитной индукции.

Основное назначение трансформаторов: изменять напряжение переменного тока.

Вопрос 2. Где используются трансформаторы?

Ответ. Трансформатор – очень распространенное устройство в электронике и электротехнике. Трансформаторы используются:

1. В сетях передачи электроэнергии.
2. В радиоэлектронных приборах (услилители низкой частоты и т.д.)
3. В источниках электропитания практически всех бытовых приборов.

Вопрос 3. Какие бывают трансформаторы?

Ответ. Трансформаторы делятся на:

• силовые;
• сварочные;
• измерительные;
• импульсные;
• разделительные;
• согласующие и т.д.

Помимо этого трансформаторы разделяют по числу фаз: однофазные, двухфазные, трехфазные и многофазные.

Вопрос 4. Из чего состоит простейший трансформатор?

Ответ. Основными элементами любого трансформатора являются изолированные обмотки, намотанные на сердечник.

Вопрос 5. Когда изобрели трансформатор?

Ответ.   Прообразом трансформатора считается индукционная катушка француза Г. Румкорфа, представленная в 1848-м. В 1876 году русский электротехник П. Н. Яблочков запатентовал трансформатор переменного тока с разомкнутым сердечником. Затем английские братья Гопкинсон, а также румыны К. Циперановский и О. Блати доработали устройство, добавив  замкнутый магнитопровод. В таком виде конструкция трансформатора остается актуальной и по сей день.

В основе работы трансформатора лежит явление электромагнитной индукции, открытое Майклом Фарадеем.

Проблемы с учебой? Обращайтесь в сервис помощи студентам в любое время!

[Решено] Когда трансформатор работает без нагрузки, первичное напряжение приложено

Когда трансформатор работает без нагрузки, первичное напряжение приблизительно уравновешено

a. Первичная ЭДС индукции

b. Вторичная ЭДС индукции

c. Напряжение на клеммах вторичной обмотки

d. Падение напряжения на сопротивлении и реактивном сопротивлении

Какое утверждение правильно?

1. Только a
2. Только a и b
3. Только c и d
4. Только d

Вариант 1: Только a

Бесплатно

CT 1: Строительные материалы

6,5 тыс. пользователей

10 вопросов

20 баллов

12 минут

Работа трансформатора без нагрузки:

Когда трансформатор работает без нагрузки, вторичная обмотка разомкнута, что означает отсутствие нагрузки на вторичной обмотке трансформатора и, следовательно, , ток во вторичной обмотке будет равен нулю.

В то время как по первичной обмотке протекает небольшой ток I ₀ , называемый током холостого хода, который составляет от 2 до 10% номинального тока.

Ток холостого хода состоит из двух составляющих:

Реактивная или намагничивающая составляющая (I _m ):

Находится в квадратуре с приложенным напряжением В ₁ . Он производит поток в сердечнике и не потребляет никакой энергии.

Активный или силовой компонент (I _w ): Он также известен как рабочий компонент.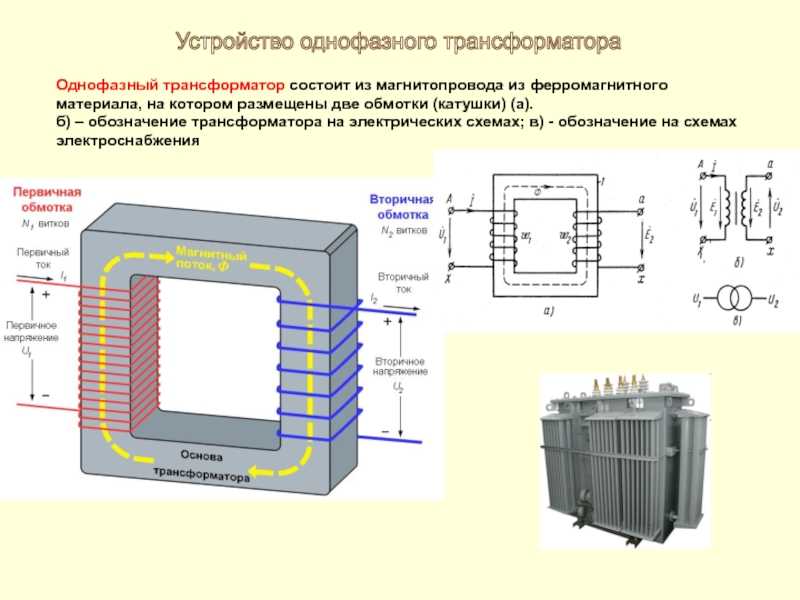 Оно находится в фазе с приложенным напряжением V ₁ . Он компенсирует потери в железе и небольшое количество первичных потерь в меди.

Векторная диаграмма:

• Функция намагничивающего компонента заключается в создании намагничивающего потока, и, таким образом, он будет находиться в фазе с потоком.
• ЭДС индукции в первичной и вторичной обмотках отстает от потока ϕ на 90 градусов.
• Первичными потерями в меди пренебрегают, а вторичные потери тока равны нулю, как I ₂ это ноль.
• Следовательно, ток I ₀ отстает от вектора напряжения V ₁ на угол ϕ ₀ , называемый углом коэффициента мощности холостого хода и показанный на векторной диаграмме.
• Приложенное напряжение V ₁ показано равным и противоположным ЭДС индукции E ₁ , поскольку разница между ними незначительна на холостом ходу.
• Активный компонент I _w совмещен по фазе с приложенным напряжением V ₁ .
• Векторная сумма тока намагничивания I _m и рабочего тока I _w дает ток холостого хода I ₀ .

 

Следовательно, когда трансформатор работает без нагрузки, приложенное к первичной обмотке напряжение приблизительно уравновешивается ЭДС первичной обмотки.

Скачать решение PDF

Поделиться в WhatsApp

Последние обновления UPSC IES

Последнее обновление: 3 марта 2023 г.

3 марта 2023 года Союзная комиссия по государственной службе опубликовала результаты предварительных испытаний UPSC IES. Экзамен был проведен 19 февраля 2023 г. по экзаменам I и II. Всего было освобождено 327 вакансий. Основной экзамен состоится 25 июня 2023 года. Кандидаты подали заявки в период с 14 сентября 2022 года по 4 октября 2022 года. Кандидаты должны соответствовать критериям приемлемости USPC IES, чтобы принять участие в наборе. Кандидаты должны попытаться пройти пробные тесты UPSC IES, чтобы повысить свою эффективность. Документы UPSC IES за предыдущий год можно скачать здесь.

Что такое напряжение холостого хода трансформатора?

\$\начало группы\$

Из какого «закона» трансформаторов получено следующее уравнение для практического трансформатора? Я предполагаю, что это не V ₁ /N ₁ = V ₂ /N ₂ , что относится только к идеальным трансформаторам.

\начать{выравнивание} V_{2,NL}&=V_1/а \end{align}

V _2,NL — напряжение холостого хода на вторичной обмотке, V ₁ — напряжение на первичной обмотке, a — коэффициент трансформации.

• напряжение
• трансформатор
• обмотка

\$\конечная группа\$

8

\$\начало группы\$

Есть старая поговорка: «Все модели ошибочны, некоторые модели полезны». Инженерия часто связана с определением того, какие эффекты необходимо учитывать, а какие можно игнорировать.

Понятие «идеальный х» не существовало бы, если бы оно не было полезным. «Идеальный х» — это самое основное приближение к «реальному х». В случае трансформатора идеальная модель возникает, когда мы строим электромагнитную модель трансформатора, используя провод с нулевым сопротивлением, намотанный на сердечник с бесконечной проницаемостью, и игнорируя емкостные эффекты.

Если «идеальный x» не является достаточно хорошей моделью, мы переходим к лучшим моделям. Распространенная модель показана ниже. Это представляет реальный трансформатор с точки зрения идеального трансформатора, трех резисторов и трех катушек индуктивности.

Изображение предоставлено: BillC на Wikimedia commons

\$R_P\$ представляет первичное сопротивление, \$X_P\$ представляет первичную индуктивность рассеяния, \$R_S\$ представляет вторичное сопротивление и \$X_S\$ представляет собой вторичную индуктивность рассеяния . \$R_C\$ представляет собой потери в сердечнике, а \$X_M\$ представляет собой намагничивающую индуктивность. Резисторы, представляющие вторичное сопротивление и утечку, были перенесены через идеальный трансформатор, чтобы упростить анализ схемы.

В идеальном трансформаторе сопротивления и индуктивности, представляющие индуктивность рассеяния и сопротивление обмотки, были бы равны нулю, а сопротивления, представляющие потери в сердечнике и ток намагничивания, были бы бесконечны.

Как это связано с «напряжением без нагрузки»?

Поскольку нагрузки нет, \$R_S\$ и \$X_S\$ не влияют на выходное напряжение. Однако \$R_P\$, \$X_P\$, \$R_C\$ и \$X_M\$ могут иметь эффект. Ток, протекающий через \$R_C\$ и \$X_M\$, вызовет падение напряжения в \$R_P\$ и \$X_P\$.

Следовательно, основное предположение вашего уравнения состоит в том, что \$R_P\$ и \$X_P\$ намного меньше, чем \$R_C\$ и \$X_M\$, и, следовательно, падение напряжения в \$R_P\$ и \$X_P\$ можно не учитывать.

\$\конечная группа\$

6

\$\начало группы\$

V ₁ /N ₁ = V ₂ /N ₂

\$\dfrac{N_1}{N_2} ~=~a\$

Это делает ваши уравнения эквивалентными для идеального трансформатора .

Практичная конструкция трансформатора имеет множество переменных для допустимого отклонения напряжения, повышения температуры при номинальной нагрузке и содержания гармоник при максимальном напряжении, близком к насыщению. Напряжение должно возбудить сердечник, чтобы взаимно соединить выход. Исходя из импеданса первичной обмотки, это составляет около 10% от номинального тока нагрузки и эффективного импеданса первичной обмотки.

Из-за стоимости меди + сердечника по сравнению со стоимостью потерянной мощности, компромисса для практичных трансформаторов, коэффициенты зависят от стоимости.

Для понижающего коэффициента 10:1 или a=10 или любого повышающего коэффициента потери должны быть компенсированы (k) более высоким выходным напряжением таким образом, чтобы реальный коэффициент = k*a для k>1

• Маленький < 100 Вт, k = 1,1
• Большой > 5 МВА k = 1,01

Это не «закон», а «эмпирическое правило», и возможны исключения.

\$\конечная группа\$

\$\начало группы\$

Из какого «закона» трансформаторов получено следующее уравнение для практического трансформатора?

«Закон трансформаторов» на самом деле является законом индукции Фарадея

Ток через первичную катушку индуктивности создаст магнитный поток (\$\phi\$) в области в соответствии с законом Ампера и собственной индуктивностью, связанной с индуктор.

Напряжение (\$V_{L_P}\$) на первичной индуктивности (\$L_P\$) формируется в соответствии с законом индукции Фарадея. Напряжение (\$V_P)\$ на индукторе будет суммой \$V_{L_P}\$ и напряжения на RC-паразитах.

$$V_{L_P}=-N_P\frac{d\phi_P}{dt}\tag{1}$$

Второй индуктор приближается к первому так, что он сталкивается с частью (k) поток от первичной катушки индуктивности. Напряжение на вторичной индуктивности будет: $$V_{L_S}=-N_S\frac{d\phi_S}{dt}$$

Вторичный поток будет \$\phi_S=k\phi_P\$, поэтому: $$V_{L_S}=-kN_S\frac{d\phi_P}{dt}\tag{2}$$

Соотношение уравнения 2 и уравнения 1 дает знакомое уравнение трансформатора.

$$\frac{V_{L_S}}{V_{L_P}}=\frac{-kN_S\frac{d\phi_P}{dt}}{-N_P\frac{d\phi_P}{dt}}= \frac{kN_S}{N_P}$$

Преобразование и преобразование \$a=\frac{N_P}{N_S}\$ воспроизводит уравнение ОП, если \$k=1\$, что почти верно для силовых трансформаторов.

$$V_{L_S}=\frac{kV_{L_P}}{a}$$

Обратите внимание, что этот результат верен для идеальных и реальных трансформаторов.