Мощность в физике — обозначение, формулы и примеры
Определение мощности
Допустим, нам необходимо убрать урожай пшеницы с поля площадью 100 га. Это можно сделать вручную или с помощью комбайна. Очевидно, что пока человек обработает 1 га площади, комбайн успеет сделать намного больше. В данном случае разница между человеком и техникой — именно то, что называют мощностью. Отсюда вытекает первое определение.
Мощность в физике — это количество работы, которая совершается за единицу времени.
Рассмотрим другой пример: между точкой А и точкой Б расстояние 15 км, которое человек проходит за 3 часа, а автомобиль может проехать всего за 10 минут. Понятно, что одно и то же количество работы они сделают за разное время. Что показывает мощность в данном случае? Как быстро или с какой скоростью выполняется некая работа.
В электромеханике эта величина имеет еще одно определение.
Мощность — это скалярная физическая величина, которая характеризует мгновенную скорость передачи энергии от системы к системе или скорость преобразования, изменения, потребления энергии.
Напомним, что скалярными величинами называются те, значение которых выражается только числом (без вектора направления).
Мощность человека в зависимости от деятельности
Вид деятельности | Мощность, Вт |
|---|---|
Неспешная ходьба | 60–65 |
Бег со скоростью 9 км/ч | 750 |
Плавание со скоростью 50 м/мин | 850 |
Игра в футбол | 930 |
Пятерка по физике у тебя в кармане!
Решай домашку по физике на изи.
Как обозначается мощность: единицы измерения
В таблице выше вы увидели обозначение в ваттах, и читая инструкции к бытовой технике, можно заметить, что среди характеристик прибора обязательно указано количество ватт. Это единица измерения механической мощности, используемая в международной системе СИ. Она обозначается буквой W или Вт.
Измерение мощности в ваттах было принято в честь шотландского ученого Джеймса Уатта — изобретателя паровой машины. Он стал одним из родоначальников английской промышленной революции.
В физике принято следующее обозначение мощности: 1 Вт = 1 Дж / 1с.
Это значит, что за 1 ватт принята мощность, необходимая для совершения работы в 1 джоуль за 1 секунду.
В каких единицах еще измеряется мощность? Ученые-астрофизики измеряют ее в эргах в секунду (эрг/сек), а в автомобилестроении до сих пор можно услышать о лошадиных силах.
Интересно, что автором этой последней единицы измерения стал все тот же шотландец Джеймс Уатт. На одной из пивоварен, где он проводил свои исследования, хозяин накачивал воду для производства с помощью лошадей. И Уатт выяснил, что 1 лошадь за секунду поднимает около 75 кг воды на высоту 1 метр. Вот так и появилось измерение в лошадиных силах. Правда, сегодня такое обозначение мощности в физике считается устаревшим.
Одна лошадиная сила — это мощность, необходимая для поднятия груза в 75 кг за 1 секунду на 1 метр. 🐴
Единицы измерения | |
|---|---|
1 ватт | 1 |
1 киловатт | 103 |
1 мегаватт | 106 |
1 эрг в секунду | 10-7 |
1 метрическая лошадиная сила | 735,5 |
Подготовка к ОГЭ по физике онлайн поможет снять стресс перед экзаменом и получить высокий балл.
Все формулы мощности
Зная определения, несложно понять формулы мощности, используемые в разных разделах физики — в механике и электротехнике.
В механике
Механическая мощность (N) равна отношению работы ко времени, за которое она была выполнена.
Основная формула:
N = A / t, где A — работа, t — время ее выполнения.
Если вспомнить, что работой называется произведение модуля силы, модуля перемещения и косинуса угла между ними, мы получим формулу измерения работы.
Если направления модуля приложения силы и модуля перемещения объекта совпадают, угол будет равен 0 градусов, а его косинус равен 1. В таком случае формулу можно упростить:
Используем эту формулу для вычисления мощности:
N = A / t = F × S / t = F × V
В последнем выражении мы исходим из того, что скорость (V) равна отношению перемещения объекта на время, за которое это перемещение произошло.
В электротехнике
В общем случае электрическая мощность (P) говорит о скорости передачи энергии. Она равна произведению напряжения на участке цепи на величину тока, проходящего по этому участку.
P = I × U, где I — сила тока, U — напряжение.
В электротехнике существует несколько видов мощности: активная, реактивная, полная, пиковая и т. д. Но это тема отдельного материала, сейчас же мы потренируемся решать задачи на основе общего понимания этой величины. Посмотрим, как найти мощность, используя вышеуказанные формулы по физике.
Задача 1
Допустим, человек поднимает ведро воды из колодца, прикладывая силу 60 Н. Глубина колодца составляет 10 м, а время, необходимое для поднятия — 30 сек. Какова будет мощность человека в этом случае?
Решение:
Найдем вначале величину работы, используя тот факт, что мы знаем расстояние перемещения (глубину колодца 10 м) и приложенную силу 60 Н.
A = F × S = 60 Н × 10 м = 600 Дж
Когда известно значение работы и времени, найти мощность несложно:
N = A / t = 600 Дж / 30 сек = 20 Вт
Задача 2
В комнате включена лампа мощностью 100 Вт. Напряжение домашней электросети — 220 В. Какая сила тока проходит через эту лампу?
Решение:
Мы знаем, что Р = 100 Вт, а U = 220 В.
Поскольку P = I × U, следовательно I = P / U.
I = 100 / 220 = 0,45 А.
Ответ: через лампу пройдет сила тока 0,45 А.
Вопросы для самопроверки
Что характеризует механическая мощность?
Какие существуют единицы измерения мощности в физике?
Какая из единиц измерения считается устаревшей?
Мощность можно назвать скалярной величиной? Что это означает?
Как из формулы нахождения мощности получить работу?
Какой буквой обозначается мощность в механике, а какой — в электротехнике?
Какую работу производит за 30 минут устройство мощностью 600 Вт?
Как узнать напряжение в сети, если мы знаем мощность подключенного к ней прибора и силу тока, проходящую через прибор?
Если в течение 1 часа автомобиль №1 едет со скоростью 60 км/ч, а автомобиль №2 — со скоростью 90 км/ч, одинаковую ли мощность они развивают в это время?
Допустим, автобус отвез пассажиров из города А в город В за 1 час.
Если он планирует вернуться в город А пустым по той же трассе и потратить на это 1 час, ему понадобится развить такую же мощность или меньшую?
Если он планирует вернуться в город А пустым по той же трассе и потратить на это 1 час, ему понадобится развить такую же мощность или меньшую?Как рассчитать потребляемую мощность двигателя
В этой статье мы разберем, что такое мощность трехфазного асинхронного двигателя и как ее рассчитать.
Понятие мощности электродвигателя
Мощность – пожалуй, самый важный параметр при выборе электродвигателя. Традиционно она указывается в киловаттах (кВт), у импортных моделей – в киловаттах и лошадиных силах (л.с., HP, Horse Power). Для справки: 1 л.с. приблизительно равна 0,75 кВт.
На шильдике двигателя указана номинальная полезная (отдаваемая механическая) мощность. Это та мощность, которую двигатель может отдавать механической нагрузке с заявленными параметрами без перегрева. В формулах номинальная механическая мощность обозначается через Р2.
Электрическая (потребляемая) мощность двигателя Р1 всегда больше отдаваемой Р2, поскольку в любом устройстве преобразования энергии существуют потери.
Основные потери в электродвигателе – механические, обусловленные трением. Как известно из курса физики, потери в любом устройстве определяются через КПД (ƞ), который всегда менее 100%. В данном случае справедлива формула:
Р2 = Р1 · ƞ
КПД в двигателях зависит от номинальной мощности – у маломощных моделей он может быть менее 0,75, у мощных превышает 0,95. Приведенная формула справедлива для активной потребляемой мощности. Но, поскольку электродвигатель является активно-реактивной нагрузкой, для расчета полной потребляемой мощности S (с учетом реактивной составляющей) нужно учитывать реактивные потери. Реактивная составляющая выражается через коэффициент мощности (cosϕ). С её учетом формула номинальной мощности двигателя выглядит так:
Р2 = Р1 · ƞ = S · ƞ · cosϕ
Мощность и нагрев двигателя
Номинальная мощность обычно указывается для температуры окружающей среды 40°С и ограничена предельной температурой нагрева.
Поскольку самым слабым местом в двигателе с точки зрения перегрева является изоляция, мощность ограничивается классом изоляции обмотки статора. Например, для наиболее распространенного класса изоляции F допустимый нагрев составляет 155°С при температуре окружающей среды 40°С.
В документации на электродвигатели приводятся данные, из которых видно, что номинальная мощность двигателя падает при повышении температуры окружающей среды. С другой стороны, при должном охлаждении двигатели могут длительное время работать на мощности выше номинала.
Мы рассмотрели потребляемую и отдаваемую мощности, но следует сказать, что реальная рабочая потребляемая мощность P (мощность на валу двигателя в данный момент) всегда должна быть меньше номинальной:
Р 2 1
Это необходимо для предотвращения перегрева двигателя и наличия запаса по перегрузке. Кратковременные перегрузки допустимы, но они ограничены прежде всего нагревом двигателя. Защиту двигателя по перегрузке также желательно устанавливать не по номинальному току (который прямо пропорционален мощности), а исходя из реального рабочего тока.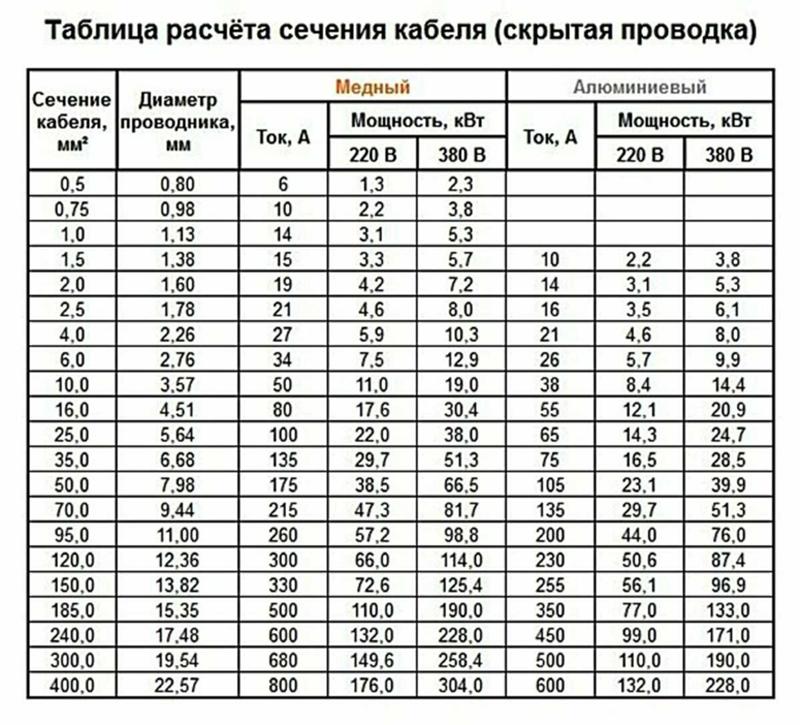
Современные производители в основном выпускают двигатели из ряда номиналов: 1,5, 2,2, 5,5, 7,5, 11, 15, 18,5, 22 кВт и т.д.
Расчет мощности двигателя на основе измерений
На практике мощность двигателя можно рассчитать, прежде всего, исходя из рабочего тока. Ток измеряется токовыми клещами в максимальном рабочем режиме, когда рабочая мощность приближается к номинальной. При этом температура корпуса двигателя может превышать 100 °С, в зависимости от класса нагревостойкости изоляции.
Измеренный ток подставляем в формулу для расчета реальной механической мощности на валу:
Р = 1,73 · U · I · cosϕ · ƞ, где
- U – напряжение питания (380 или 220 В, в зависимости от схемы подключения – «звезда» или «треугольник»),
- I – измеренный ток,
- cosϕ и ƞ – коэффициент мощности и КПД, значения которых можно принять равными 0,8 для маломощных двигателей (менее 5,5 кВт) или 0,9 для двигателей мощностью более 15 кВт.
Если нужно найти номинальную мощность
двигателя, то полученный результат округляем в бОльшую сторону до ближайшего значения из ряда номиналов.
Р2 > Р
Если необходимо рассчитать потребляемую активную мощность, используем следующую формулу:
Р1 = 1,73 · U · I · ƞ
Именно активную мощность измеряют счетчики электроэнергии. В промышленности для измерения реактивной (и полной мощности S) применяют дополнительное оборудование. При данном способе можно не использовать приведенную формулу, а поступить проще – если двигатель подключен в «звезду», измеренное значение тока умножаем на 2 и получаем приблизительную мощность в кВт.
Расчет мощности при помощи счетчика электроэнергии
Этот способ прост и не требует дополнительных инструментов и знаний. Достаточно подключить двигатель через счетчик (трехфазный узел учета) и узнать разницу показаний за строго определенное время. Например, при работе двигателя в течении часа разница показаний счетчика будет численно равна активной мощности двигателя (Р
Другие полезные материалы:
Степени защиты IP
Трехфазный двигатель в однофазной сети
Типичные неисправности электродвигателей
Что означает «В силу»?
спросил по математике к Нетбол (2,4 тыс. баллов)- математика
- сила
- круто
- прочее
- лол
прокомментировал к йокия
— это сколько раз ты повторяешь это число. например, 10 в степени двойки равно 100 bc 10×10 (2 раза) равно 100. скажи мне, имеет ли это смысл, лол
прокомментировал к анонимный
прокомментировал к анонимный
Делает общее благовоние
прокомментировал к анонимный
достаточно с
прокомментировал к да
НЕ ПОНИМАЮ
прокомментировал к анонимный
прокомментировал к анонимный
прокомментировал к анонимный
прокомментировал к неизвестно >:D
прокомментировал к анонимный
прокомментировал к …
хммм
прокомментировал к анонимный
это несколько центов
прокомментировал к анонимный
1000%
ДА
прокомментировал к анонимный
Так и есть, лол
комментариев к анонимный
дает итого без
прокомментировал к анонимный
прокомментировал к анонимный
прокомментировал к анонимный
прокомментировал к анонимный
прокомментировал к анонимный
прокомментировал к анонимный
Если бы у вас было 10x10x10 действительно меня в степени три. Или другим способом было бы просто посчитать нули, чтобы знать.
прокомментировал к собачьи дети
+1 голос
+1 голос
+1 голос
+1 голос
+1 голос
+1 голос
ответил к ❎✳ПринцессаКотята✳❎ (278 тыс. баллов)«В степени» представляет показатели степени
5+5=10 (5+5)
5×5=25 (5+5+5+5+5)
5 в степени 5=125 (5x5x5x5x5) (5+5+5+5+5+5+5+5+5+5+5+5+5+5+5+5+5+5+5+5+5+5+5+5+5 )
Экспоненты относятся к умножению так же, как умножение к сложению 9), а затем число, обозначающее показатель степени, а число после него — показатель степени
.
+2 голоса
ответил к вещьВы умножаете число само на себя, а число «в степени» равно тому, сколько раз вы умножаете его само на себя. Например, 2 в степени 3 равно 8.
прокомментировал к анонимный
прокомментировал к неизвестно >:D
+2 голоса
прокомментировал к ЛунаЛайт (159 тыс. баллов)
прокомментировал к l0st юг (14,3 тыс. баллов)
прокомментировал к братан
+2 голоса
прокомментировал к ЛунаЛайт (159 тыс. баллов)
Нет. 2+2+2+2 = 8, не умножение. 2×2 равно 4, 4×2 равно 8, затем 8×2 равно 16.
+2 голоса
ответил к анонимныйЭто означает добавить, что много нулей в конце работает только для 10 и выше Пример один в степени двойки равен 1 10 в степени 2 равен 1000
прокомментировал к ЛунаЛайт (159 тыс. баллов)
прокомментировал к анонимный
Страница:
- 1
- 2
- следующий »
Экспоненты
показатель степени числа говорит сколько раз использовать число при умножении.
В 8 2 «2» говорит о том, что 8 нужно использовать дважды при умножении,
так 8 2 = 8 × 8 = 64
Прописью: 8 2 можно было бы назвать «8 в степени 2» или «8 во второй степени», или просто «8 в квадрате»
Еще несколько примеров:Пример:
5 3 = 5 × 5 × 5 = 125- Словами: 5 3 можно назвать «5 в третьей степени», «5 в степени 3» или просто «5 куб»
Пример:
2 4 = 2 × 2 × 2 × 2 = 16- Прописью: 2 4 можно было бы назвать «2 в четвертой степени» или «2 в степени 4» или просто «2 к 4-му»
Экспоненты облегчают запись и использование многих умножений
Пример: 9 6 легче писать и читать, чем 9 × 9 × 9 × 9 × 9 × 9
Примечание.
94 = 2 × 2 × 2 × 2 = 16
Отрицательные показатели
Отрицательный? Что может быть противоположным умножению? Разделение!
Итак, мы каждый раз делим на число, что равносильно умножению на 1 число
Пример: 8 -1 = 1 8 = 0,125
Мы можем продолжить так:
Пример: 5 -3 = 1 5 × 1 5 × 1 5 = 0,008
Но часто проще сделать так:
5 -3 также можно рассчитать, как:
1 5 × 5 × 5 = 1 5 3 = 5 3 = 5 3 = 5 3 5 3 5 3 5 3 5 3 . Последний пример показал более простой способ обработки отрицательных показателей: Другие примеры:
Отрицательный? Переверни позитив!
Отрицательная экспонента Обратная величина
Положительная экспонента Ответить 4 -2 = 1 / 4 2 = 1/16 = 0,0625 10 -3 = 1 / 10 3 = 1/1000 = 0,001 (-2) -3 = 1 / (-2) 3 = 1/(-8) = -0,125
Что делать, если показатель степени равен 1 или 0?
| 1 | Если показатель степени равен 1, то у вас есть только само число (пример 9 1 = 9 ) | |
| 0 | Если показатель степени равен 0, то вы получаете 1 (пример 9 0 = 1 ) | |
А как насчет 0 0 ? Это может быть либо 1, либо 0, поэтому люди говорят, что это «неопределенное» . |
Все имеет смысл
Если вы посмотрите на эту таблицу, вы увидите, что положительный, нулевой или отрицательные показатели на самом деле являются частью одного и того же (довольно простого) шаблона:
| Пример: Степени числа 5 | |||
|---|---|---|---|
| .. и т.д.. | |||
| 5 2 | 5 × 5 | 25 | |
| 5 1 | 5 | 5 | |
| 5 0 | 1 | 1 | |
| 5 -1 | 1 5 | 0,2 | |
| 5 -2 | 1 5 × 1 5 | 0,04 | |
. | |||