Как найти Объем Параллелепипеда?
Поможем понять и полюбить математику
Начать учиться
В 5 классе ученики знакомятся с объемными фигурами. Оглянитесь вокруг — мир состоит из параллелепипедов. Так что в любой непонятной ситуации просто ищите их объём. Давай научимся это делать. В статье найдете все необходимые формулы и правила.
Понятие объема
Чтобы без труда вычислить объём любой фигуры, нужно разобраться с определениями.
Объём — это количественная характеристика пространства, занимаемого телом или веществом.
Другими словами, это то, сколько места занимает предмет.
Объём измеряется в единицах измерения размера пространства, занимаемого телом, то есть в кубических метрах, кубических сантиметрах, кубических миллиметрах.
За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (см
Объём всегда выражается в положительных числах. Это число показывает, какое именно количество единиц измерения есть в теле. Например, сколько воды в бассейне, сока в графине, земли в клумбе.
Два свойства объёма
|
Любое объемное тело имеет объем. Получается, при желании мы можем вычислить объем кружки, смартфона, вазы, кота — чего угодно.
Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Объем прямоугольного параллелепипеда
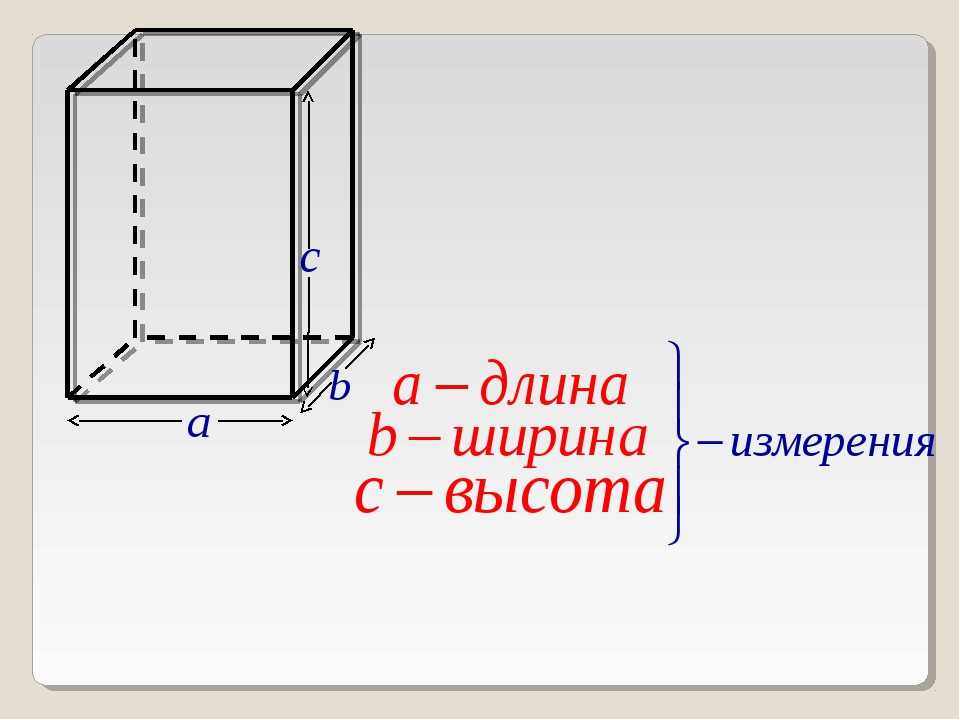
Параллелепипед — это многогранник с шестью гранями, каждая из которых является параллелограммом.
Прямоугольным параллелепипедом называют параллелепипед, у которого все грани являются прямоугольниками.
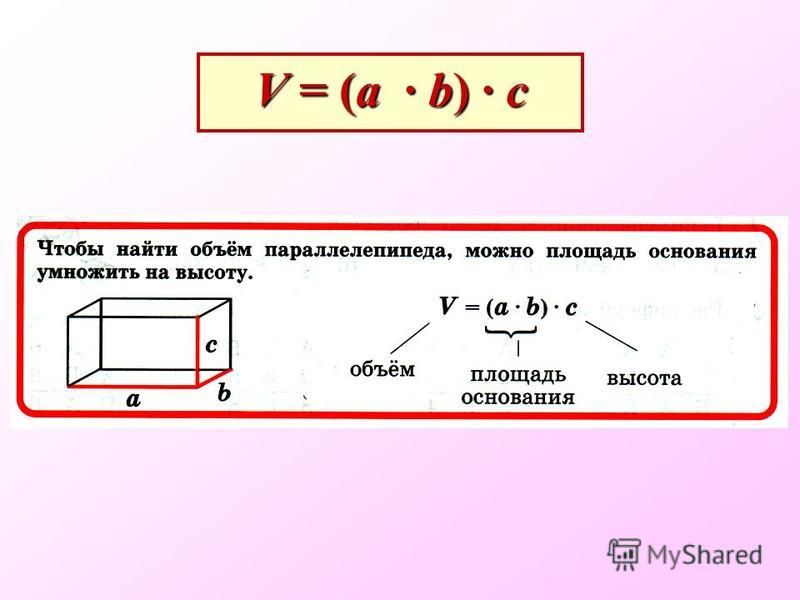
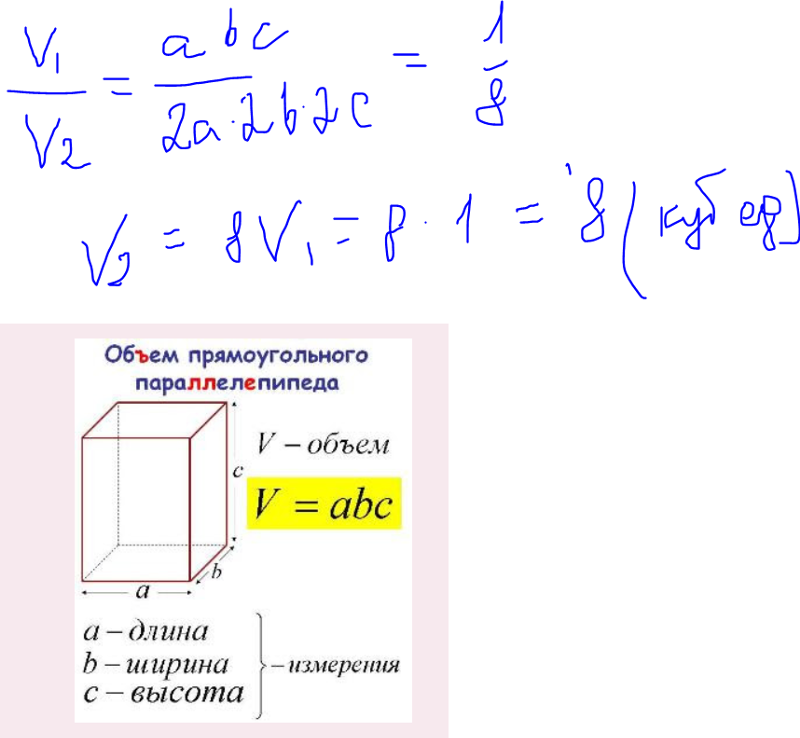
Формула объема прямоугольного параллелепипеда Чтобы вычислить объем прямоугольного параллелепипеда, найдите произведение его длины, ширины и высоты: V = a × b × h |
Чтобы не запутаться в формулах, запоминайте табличку с условными обозначениями.
a | длина параллелепипеда |
b | ширина параллелепипеда |
h | высота параллелепипеда |
P (осн) | периметр основания |
S (осн) | площадь основания |
S (бок) | площадь боковой поверхности |
S (п. | площадь полной поверхности |
V | объем |
Пример 1. Чему равен объем параллелепипеда со сторонами 9 см, 6 см, 3 см.
a = 9 см
b = 6 см
h = 3 см
V = a × b × h
V = 9 × 6 × 3 = 162 см3.
Ответ: объем прямоугольного параллелепипеда равен 162 см3.
Следствие Объем параллелепипеда равен произведению площади основания на высоту. V = Sосн × h |
Из этого следствия выведем формулу нахождения площади основания параллелепипеда.
Sосн = V : h
Пример 2. Найдите площадь основания параллелепипеда, если его объем равен 96 см3, а высота 8 см.
V = 96 см3
h = 8 см
V = Sосн × h
Sосн = V : h
Sосн = 82 см3 : 8 см = 12 см2.
Ответ: площадь основания параллелепипеда равна 12 см2.
Обучение на курсах по математике в онлайн-школе Skysmart поможет быстрее разобраться в теме и правильно решать задачки!
Вычисление площади
Как вы уже поняли, вычисление объёма параллелепипеда напрямую зависит от вычисления его площади. Давайте разберемся, сколько всего площадей можно найти в параллелепипеде.Чтобы найти площадь боковой поверхности параллелепипеда, вычислите по отдельности площадь каждой боковой грани, а затем найдите сумму получившихся значений.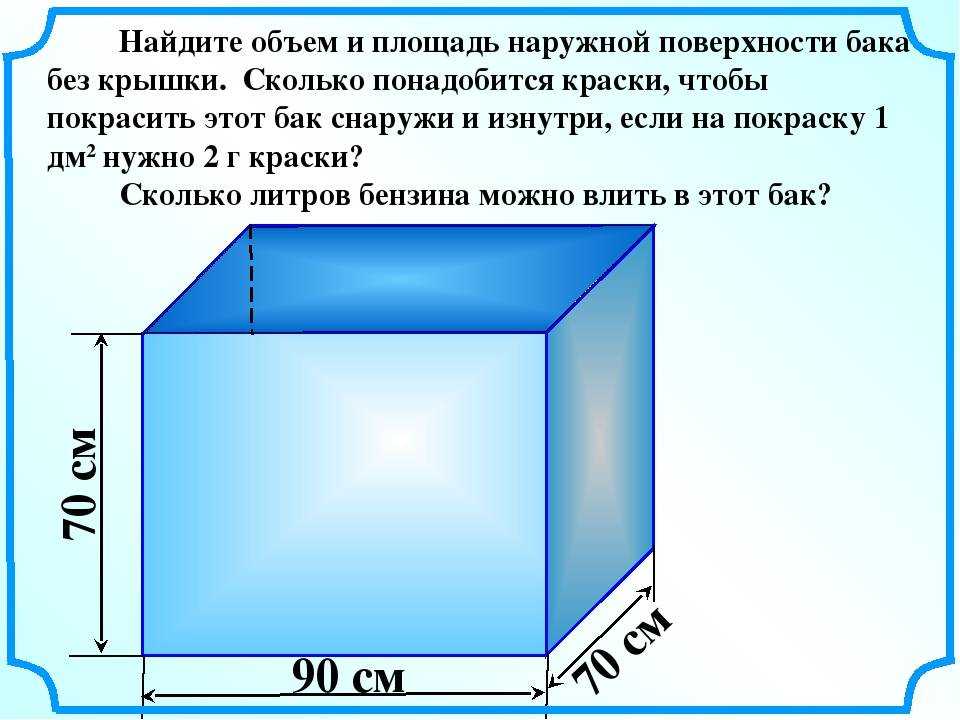
Так как противолежащие грани прямоугольного параллелепипеда одинаковые, то получим формулу:
- Sб. п. = 2 (ac + bc)
Чтобы вычислить площадь полной поверхности параллелепипеда, сложите площадь боковой поверхности и две площади основания. Так как площади оснований у прямоугольного параллелепипеда одинаковые, то получим формулу:
- Sп. п. = 2 (ab + ac + bc)
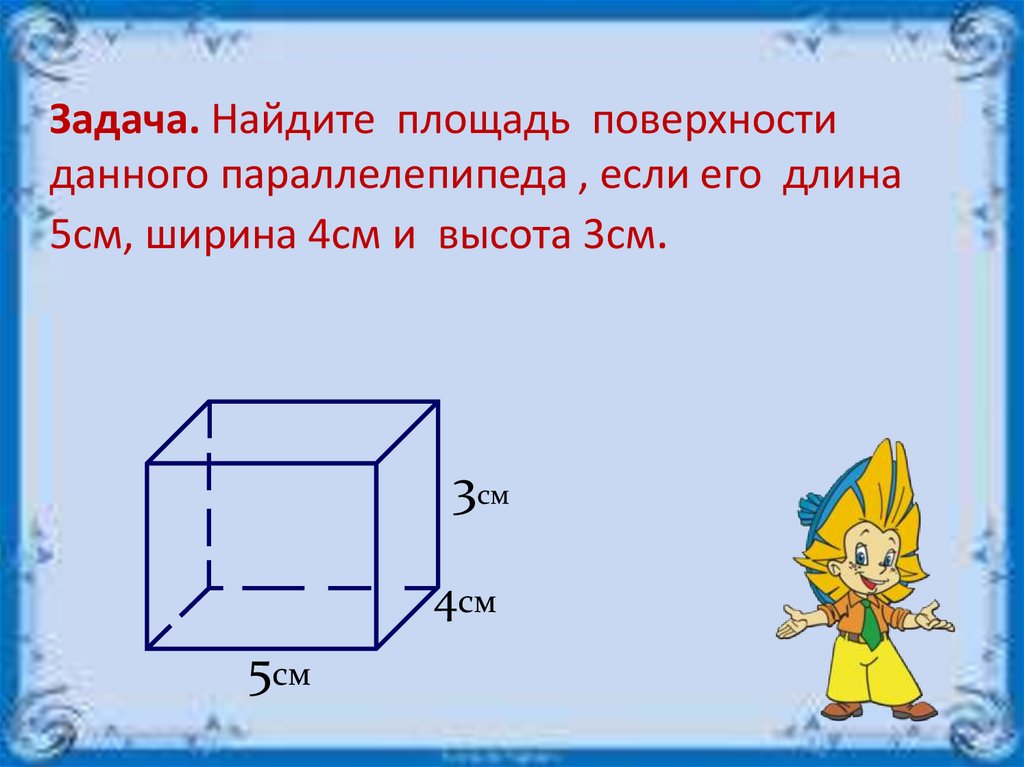
Пример 3. Найдем площадь поверхности параллелепипеда, если длина основания равна 6 сантиметров, ширина — 4 см соответственно, а высота — 3 см.
Sп. п. = 2 (ab + ac + bc)
Sп. п. = 2 (6 × 4 + 6 × 3 + 4 × 3) = 2 × (24 + 18 + 12) = 2 × 54 = 108 см2.
Ответ: площадь поверхности параллелепипеда — 108 см2.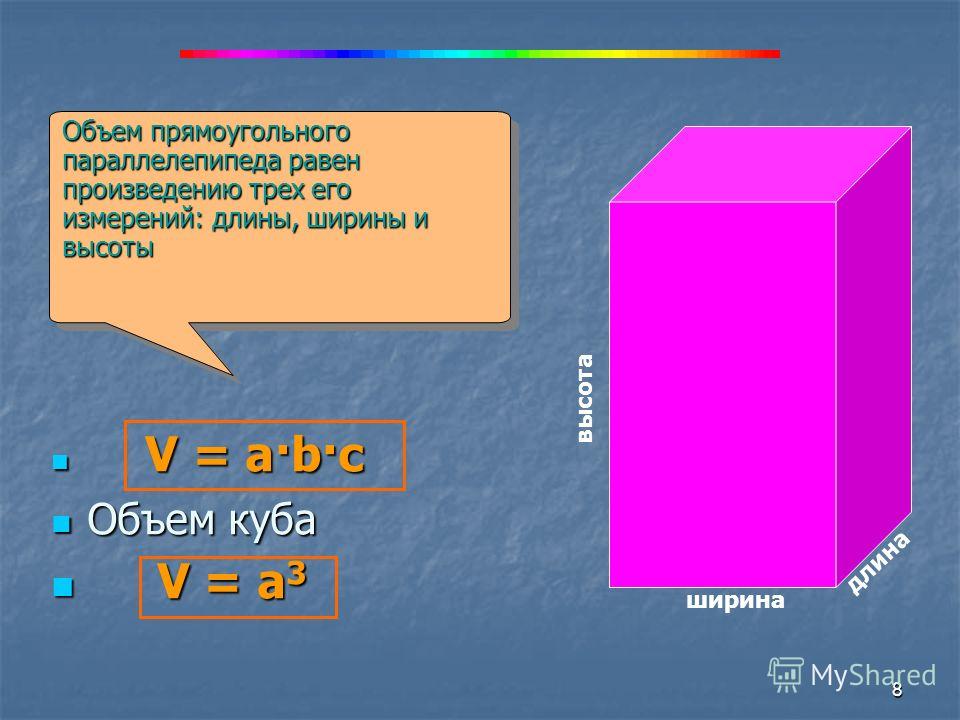
Как видите, вычислить объём и найти площадь параллелепипеда совсем не трудно.
Бесплатные занятия по английскому с носителем
Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.
Задачи на самопроверку
Пользоваться онлайн-калькуляторами можно, когда вы уже натренировались в решении задачек и с закрытыми глазами можете вычислить объем любого параллелепипеда. Давайте разберем еще несколько примеров.
Задачка 1. Найдите объём параллелепипеда со сторонами 18 см, 10 см, 7 см.
Как решаем:
a = 18 см
b = 10 см
h = 7 см
Формула нахождения объема параллелепипеда:
V = a × b × h
Подставляем наши числа:
V = 18 × 10 × 7 = 1260 см3.
Ответ: объём параллелепипеда равен 1260 см3.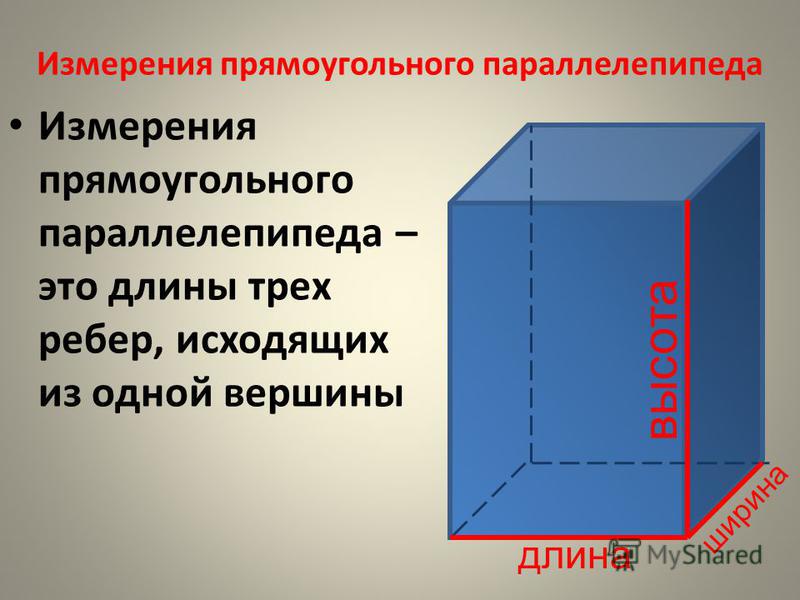
Задачка 2. Найдите площадь основания параллелепипеда, если его объём равен 120 см3, а высота — 15 см.
Как решаем:
V = 120 см
h = 15 см
Sосн = V : h
Sосн = 120 см3: 15 см = 8 см2.
Ответ: площадь основания параллелепипеда равна 8 см2.
Задачка 3. Найдите площадь полной поверхности прямоугольного параллелепипеда, если длина основания равна 30 сантиметров, ширина равна 12 см, а высота равна 5 см.
Как решаем:
Sп. п. = 2 (ab + ac + bc)
Sп. п. = 2 (30 × 12 + 30 × 5 + 12 × 5) = 2 × (360 + 150 + 60) = 2 × 570 = 1140 см2.
Ответ: площадь полной поверхности параллелепипеда равна 1140 см2.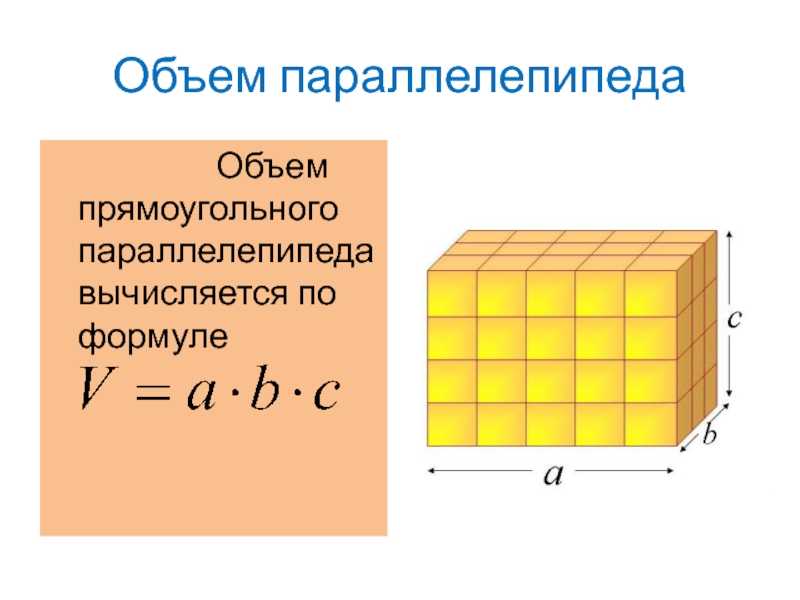
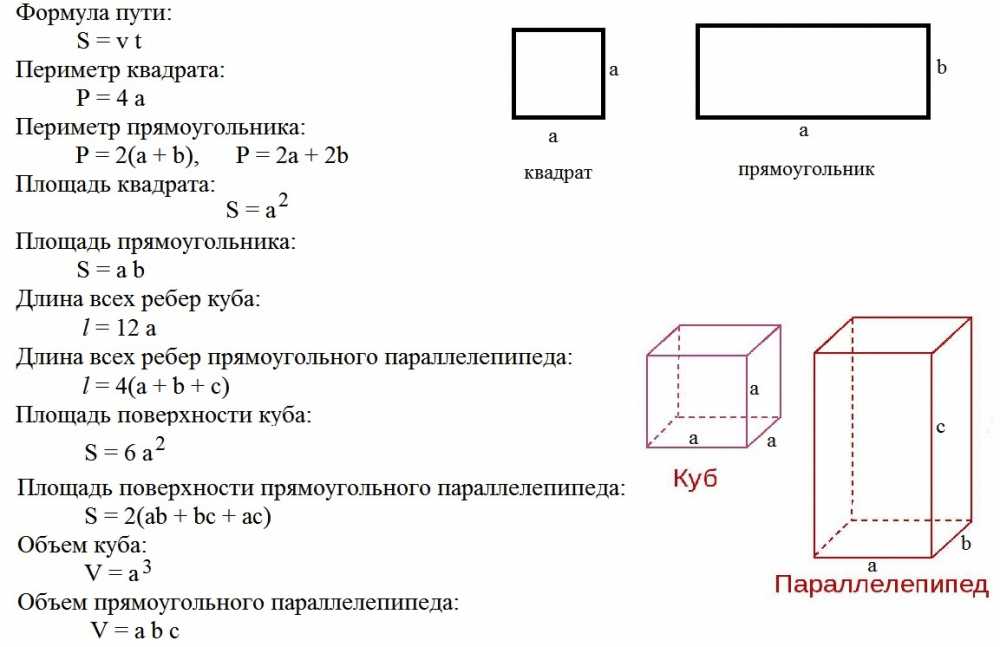
Пусть все необходимые формулы будут под рукой в нужный момент. Сохраняйте табличку-шпаргалку на гаджет или распечатайте ее и храните в учебнике.
V параллелепипеда | V = a × b × h |
| V = Sосн × h |
S боковой поверхности | Sб. п. = 2 (ac + bc) |
S полной поверхности | Sп. п. = 2 (ab + ac + bc) |
Шпаргалки по математике родителей
Все формулы по математике под рукой
Анастасия Белова
К предыдущей статье
341.
Время, скорость, расстояние
К следующей статье
380.6K
Порядок действий в математике
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Рассчитать объем коробки в м3 и литрах онлайн
07.10.2019
Сколько будет стоить отправка вашего груза до места назначения? Чтобы ответить на это вопрос, нужно знать его объем в кубических метрах, т. к. транспортные компании чаще всего в прайсе указывают стоимость услуг именно в таких единицах измерения.
Картонные коробки — наиболее выгодный и удобный вид упаковки для большинства товаров.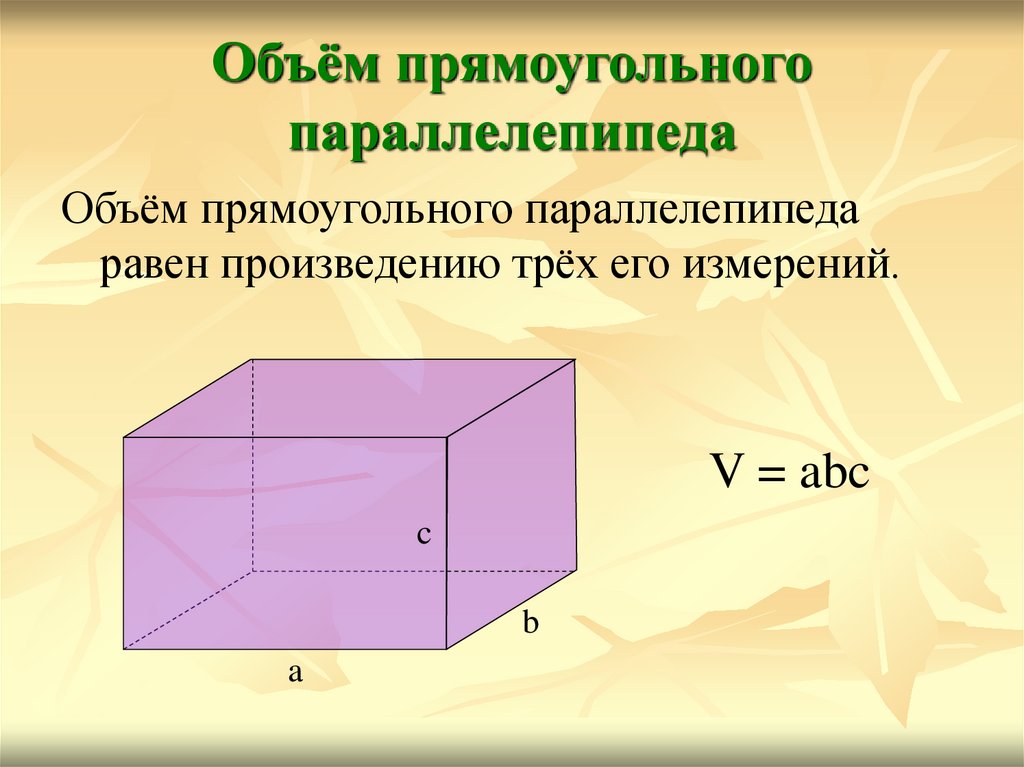 Выбирая гофроупаковку для своей продукции, вам нужно, в первую очередь, рассчитать объем коробок и заказать нужное количество коробок, чтобы не перевозить воздух и не переплачивать за транспортные услуги.
Выбирая гофроупаковку для своей продукции, вам нужно, в первую очередь, рассчитать объем коробок и заказать нужное количество коробок, чтобы не перевозить воздух и не переплачивать за транспортные услуги.
Если в результате расчета оказалось, что вам требуется гофротара индивидуальных размеров, наша компания «МС-ПАК» изготовит нужный тираж на заказ. Рассмотрим, как правильно рассчитать объем картонной коробки.
Поэтапный расчет объема картонной коробки
Для расчета нужно:
- Измерить длину а и ширину b, если дно коробки квадратное, то а=b;
- Измерить высоту h как расстояние от нижнего до верхнего клапана коробки.
Сначала нужно рассчитать внутренний объем коробки, необходимый для размещения груза. Габаритные размеры груза должны быть на 5–10 мм меньше, чем внутренние размеры гофроупаковки.
Формула для вычисления объема V в м3 коробки с прямоугольным или квадратным основанием:
V=a*b*h
где a – длина основания (м), b – ширина основания (м),
h – высота коробки (м).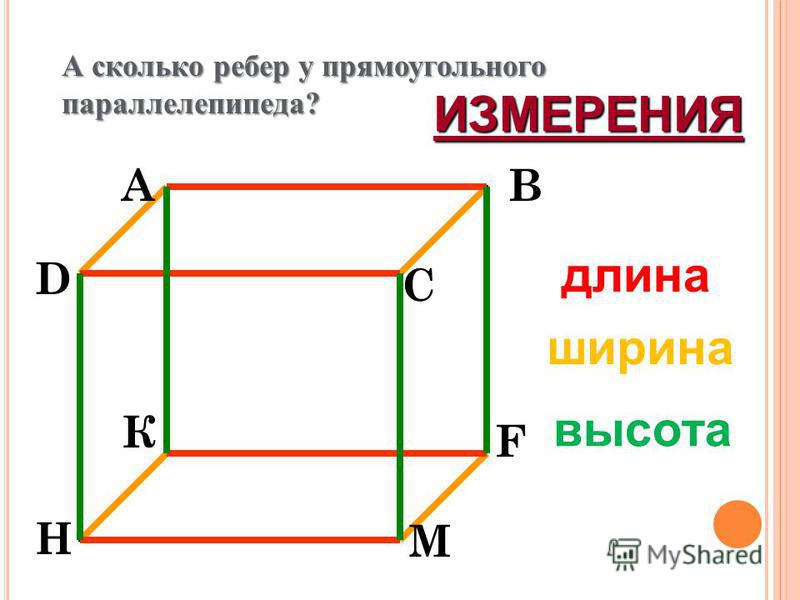
Если в основании коробки не прямоугольник, а треугольник, пяти- или шестиугольник, то формула вычисления объема будет:
V=S*h
где S — площадь основания коробки, а h — ее высота.
Объем, занимаемый заготовкой (коробкой) (с учетом толщины стенок) рассчитывается для правильного размещения внутри транспортного средства или хранения на складе.
Формула для расчета занимаемого объема:
V=Площадь (S) * толщину листа
*как рассчитать площадь (S) картонной коробки — в этой статье
| Тип: | Профиль: | Толщина (мм): |
| Трехслойный гофрокартон | B | 3 |
| Трехслойный гофрокартон | C | 3,7 |
| Трехслойный гофрокартон | E | 1,6 |
| Пятислойный гофрокартон | BC | 7 |
| Пятислойный гофрокартон | BE | 4 |
Перемножив полученные значения, получим объем коробки в кубических метрах. Чтобы получить результат в литрах необходимо полученное значение в м3 умножить на 1000.
Чтобы получить результат в литрах необходимо полученное значение в м3 умножить на 1000.
Рассчитать объем коробки в м
3 и литрах онлайнДля обычных коробок в форме куба или параллелепипеда (со сторонами в виде квадратов или прямоугольников) на нашем сайте есть онлайн-калькулятор, который ускорит расчет.
Длина, мм
Ширина, мм
Высота, мм
Внутренний объем коробки
м3
литров
Длина, мм
Ширина, мм
Высота, мм
Тип картона Трехслойный картон (B)Трехслойный картон (C)Трехслойный картон (E)Пятислойный картон (BC)Пятислойный картон (BE)
Объем занимаемый заготовкой(коробкой)
м3
литров
Пример расчета
После измерения получены значения: а=600 мм, b=400 мм, h= 400 мм.
Переводим их в метры: а=600/1000=0,6 м, b=400/1000=0,4 м, h=400/1000=0,4 м.
Подставляя полученные результаты в формулу для расчета объема, получим значение: V=a*b*h=0,6*0,4*0,4=0,096 м3.
Если в коробки фасуются сыпучие или жидкие грузы, то для расчета необходимого объема используем соотношение 1 м3 = 1000 л и, умножив полученное значение объема в м3 на 1000, получим объем в литрах.
Для нашего примера объем коробки (внутренний) в литрах равен 0,096*1000=96 литров.
Расчет объема | SkillsYouNeed
На этой странице объясняется, как рассчитать объем твердых предметов, т.е. сколько вы могли бы вместить в предмет, если, например, вы наполнили его жидкостью.
Площадь — это мера того, сколько места находится внутри двухмерного объекта (дополнительную информацию см. на нашей странице: Расчет площади).
Объем — это мера пространства внутри трехмерного объекта. Наша страница о трехмерных фигурах объясняет основы таких фигур.
В реальном мире вычисление объема, вероятно, не будет использоваться так часто, как вычисление площади.
Тем не менее, это может быть важно. Возможность рассчитать объем позволит вам, например, определить, сколько места у вас есть для упаковки при переезде, сколько офисного пространства вам нужно или сколько варенья вы можете поместить в банку.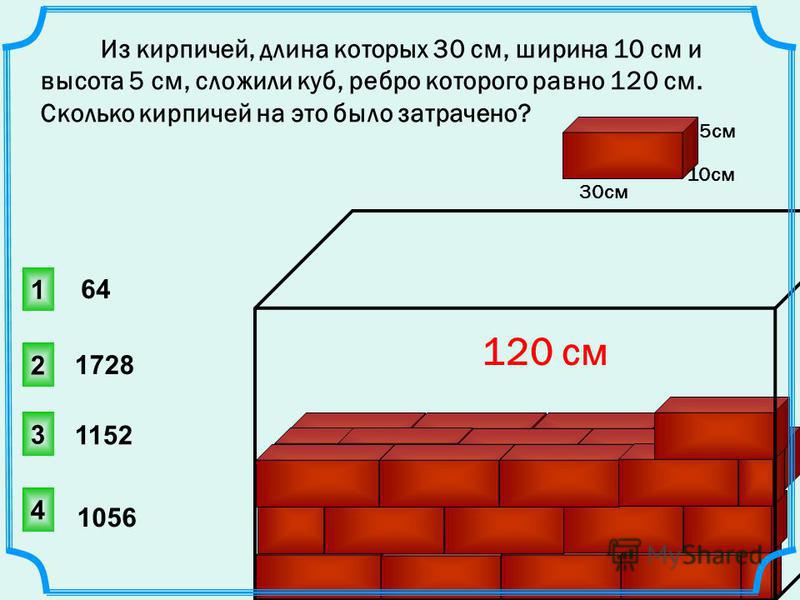
Это также может быть полезно для понимания того, что имеют в виду СМИ, когда говорят о мощности плотины или расходе реки.
Примечание по единицам измерения
Площадь выражается в квадратных единицах ( 2 ), поскольку она измеряется в двух измерениях (например, длина × ширина).
Объем выражается в кубических единицах ( 3 ), поскольку он измеряется в трех измерениях (например, длина × ширина × глубина). Кубические единицы включают см3, м3 и кубические футы. Кубические единицы включают 3 см, 3 м и кубические футы.
ВНИМАНИЕ!
Объем также может быть выражен как емкость по жидкости.
Метрическая система
В метрической системе вместимость жидкости измеряется в литрах, что напрямую сравнимо с кубическим измерением, поскольку 1 мл = 1 см 3 . 1 литр = 1000 мл = 1000 см 3 .
Имперская/английская система
В имперской/английской системе эквивалентными единицами измерения являются жидкие унции, пинты, кварты и галлоны, которые нелегко перевести в кубические футы. Поэтому лучше всего придерживаться либо жидких, либо твердых единиц объема.
Поэтому лучше всего придерживаться либо жидких, либо твердых единиц объема.
Для получения дополнительной информации см. нашу страницу о системах измерения.
Основные формулы для вычисления объема
Объем тел, основанных на прямоугольниках
В то время как основная формула площади прямоугольной формы равна длине × ширине, основная формула для объема равна длине × ширине6 ×
высота.
То, как вы ссылаетесь на различные измерения, не влияет на расчет: вы можете, например, использовать «глубину» вместо «высоты». Важно то, что три измерения умножаются вместе. Вы можете умножать в любом порядке, поскольку это не изменит ответ (см. нашу страницу на умножить на для большего).
Коробка с размерами 15 см в ширину, 25 см в длину и 5 см в высоту имеет объем:
15 × 25 × 5 = 1875 см для покрытия объема цилиндров и призм тоже.Вместо прямоугольного конца у вас просто другая форма: круг для цилиндров, треугольник, шестиугольник или любой другой многоугольник для призмы.
Фактически, для цилиндров и призм объем равен площади одной стороны, умноженной на глубину или высоту формы.
Таким образом, основная формула для объема призм и цилиндров:
Площадь торца × высота/глубина призмы/цилиндра.
Остерегайтесь несовместимых единиц!
Прямой отрезок круглой трубы имеет внутренний диаметр 2 см и длину 1,7 м. Рассчитайте объем воды в трубе.
В этом примере вам нужно рассчитать объем очень длинного тонкого цилиндра, образующего внутреннюю часть трубы. Площадь одного конца можно рассчитать по формуле площади круга πr 2 . Диаметр 2см, значит радиус 1см. Таким образом, площадь равна π × 1 2 , что составляет 3,14 см 2 .
Длина трубы 1,7 м, поэтому вам нужно умножить площадь конца на длину, чтобы найти объем.
Остерегайтесь несовместимых юнитов! Площадь в сантиметрах, а длина в метрах. Сначала преобразуйте длину в см 1,7 × 1000 = 1700 см.
Таким образом, объем равен 3,14 × 1700 = 5338 см 3 . Это эквивалентно 5,338 литра или 0,0053 м 3 .
Объем конусов и пирамид
Тот же принцип, что и выше (ширина × длина × высота), применяется для расчета объема конуса или пирамиды, за исключением того, что, поскольку они сходятся в точке, объем составляет лишь долю сумма, которая была бы, если бы они продолжали иметь ту же форму (поперечное сечение) насквозь.
Объем конуса или пирамиды составляет ровно одну треть объема коробки или цилиндра с таким же основанием.
Таким образом, формула выглядит следующим образом:
Площадь основания или торца × высота конуса/пирамиды × 1 / 3
Если не можете, вернитесь на нашу страницу
0 0 Расчет площади помните, как вычислить площадь круга или треугольника.Например, чтобы вычислить объем конуса с радиусом 5 см и высотой 10 см:Площадь внутри круга = πr 2 (где π (пи) приблизительно равно 3,14, а r — радиус круг).
В этом примере площадь основания (круга) = πr 2 = 3,14 × 5 × 5 = 78,5 см 2 .
78,5 × 10 = 785
785 × 1/3 = 261,6667 см 3
Объем сферы
Как и в случае с кругом, для вычисления объема сферы требуется π (пи).
Формула 4/3 × π × радиус 3 .
Вам может быть интересно, как можно вычислить радиус мяча. Если не считать протыкания вязальной спицы (эффективно, но смертельно для мяча!), есть более простой способ.
Расстояние вокруг самой широкой точки сферы можно измерить напрямую, например, рулеткой. Этот круг является окружностью и имеет тот же радиус, что и сама сфера.
Длина окружности рассчитывается как 2 x π x радиус.
Чтобы вычислить радиус по длине окружности:
Разделите длину окружности на (2 x π) .
Примеры работы: Расчет объема
Расчет объема неправильных тел
Точно так же, как вы можете рассчитать площадь неправильных двумерных фигур, разбив их на правильные, вы можете сделать то же самое, чтобы вычислить объем неправильных тел. Просто разделите тело на более мелкие части, пока не получите только многогранники, с которыми вам будет легко работать.
Дальнейшее чтение из книги «Навыки, которые вам нужны»
Понимание геометрии
Часть руководства «Навыки, которые вам необходимы для счета»В этой электронной книге рассматриваются основы геометрии и рассматриваются свойства форм, линий и твердых тел. Эти концепции построены в книге, с примерами работы и возможностями для вас, чтобы попрактиковаться в ваших новых навыках.
Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас.
В заключение…
Используя эти принципы, если необходимо, теперь вы сможете рассчитать объем почти всего в вашей жизни, будь то упаковочный ящик, комната или цилиндр с водой.
Калькулятор объема цилиндра
Автор: Ханна Памула, доктор философии
Рецензия: Богна Шик и Джек Боуотер
Последнее обновление: 06 сентября 2022 г.
Содержание:
- Как рассчитать объем цилиндра?
- Объем полого цилиндра
- Объем наклонного цилиндра
- Часто задаваемые вопросы
Наш калькулятор объема цилиндра позволяет вычислить объем этого тела. Если вы хотите выяснить, сколько воды помещается в банку, кофе в вашу любимую кружку или даже объем соломинки для питья — вы находитесь в правильном месте. Другой вариант расчета объем цилиндрической оболочки (полый цилиндр).
Как рассчитать объем цилиндра?
Начнем с самого начала – что такое цилиндр? Это твердое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями. Мы можем представить его как твердую физическую банку с крышками сверху и снизу. Для расчета его объема нам необходимо знать два параметра – радиус (или диаметр) и высоту:
объем цилиндра = π × радиус цилиндра² × высота цилиндраКалькулятор объема цилиндра помогает найти объем прямого, полого и наклонного цилиндра:
Объем полого цилиндра
Полый цилиндр, также называемый цилиндрической оболочкой, представляет собой трехмерную область, ограниченную двумя прямыми круговыми цилиндрами.
с одной осью и двумя параллельными кольцевыми основаниями, перпендикулярными общей оси цилиндров.
Легче понять это определение, представив, например, соломинку для питья или трубку – полый цилиндр – это пластик, металл или другой материал. Формула объема полого цилиндра:
объем_цилиндра = π × (R² - r²) × высота_цилиндрагде
R– внешний радиус, аr– внутренний радиусДля расчета объема цилиндрической оболочки возьмем пример из реальной жизни. , может… рулон туалетной бумаги, а почему бы и нет? 😀
Введите внешний радиус цилиндра . Стандарт равен примерно 5,5 см.
Определить внутренний радиус цилиндра . Это внутренний радиус картонной детали около 2 см.
Узнать высоту цилиндра ; для нас это 9 см.
Тадаам! Объем полого цилиндра равен 742,2 см³.
Помните, что результатом является объем бумаги и картона.
Если вы хотите посчитать, сколько пластилина можно положить внутрь картонного рулона, воспользуйтесь стандартной формулой объема цилиндра — калькулятор посчитает в мгновение ока!
Объем косого цилиндра
Косой цилиндр – это тот, который «наклоняется» – стороны не перпендикулярны основаниям, в отличие от стандартного «прямого цилиндра». Как рассчитать объем косого цилиндра? Формула такая же, как и для прямого. Только помните, что высота должна быть перпендикулярна основаниям.
Теперь, когда вы знаете, как рассчитать объем цилиндра, возможно, вы захотите определить объемы других трехмерных тел? Используйте этот общий калькулятор объема!
Если вам интересно, сколько чайных ложек или чашек поместится в ваш контейнер, воспользуйтесь нашим конвертером объема.
Для расчета объема грунта, необходимого для цветочных горшков различной формы, в том числе для цилиндрического, воспользуйтесь калькулятором грунта.
Часто задаваемые вопросы
Где можно найти цилиндры в природе?
Цилиндры вокруг нас , и мы говорим не только о банках Pringles.
Хотя вещи в природе редко бывают идеальными цилиндрами, некоторые примеры стволы деревьев и стебли растений, некоторые кости (и, следовательно, тела) и жгутики микроскопических организмов. Они составляют большое количество природных объектов на Земле!
Как нарисовать цилиндр?
Чтобы нарисовать цилиндр, выполните следующие действия:
Нарисуйте слегка приплюснутый круг. Чем более он сплющен, тем ближе вы смотрите на сторону цилиндра на .
Начертить две равные параллельные линии с дальних сторон вашего круга спускается вниз.
Соедините концы двух линий полукруглой линией, которая выглядит так же, как нижняя половина вашего верхнего круга.
При необходимости добавьте тень и штриховку.
Как рассчитать вес цилиндра?
Для расчета веса баллона:
Возведение в квадрат радиуса цилиндра .
Умножьте квадрат радиуса на число пи и высоту цилиндра .
Умножьте объем на плотность цилиндра. Результат – вес цилиндра.
Как рассчитать отношение площади поверхности к объему цилиндра?
Найдите объем цилиндра по формуле πr²h .
Найдите площадь поверхности цилиндра по формуле 2πrh + 2πr² .
Из двух формул составьте отношение , то есть πr²h : 2πrh + 2πr².
В качестве альтернативы упростите его до rh : 2(h+r) .
Разделите с обеих сторон на одну из сторон, чтобы получить соотношение в его простейшей форме.
Как найти высоту цилиндра?
Если у вас объем и радиус цилиндра:
- Убедитесь, что объем и радиус указаны в одинаковых единицах (например, см³ и см), а радиус — в радианах .
- Квадрат радиус.
- Разделите объем на квадрат радиуса и число Пи, чтобы получить высоту в тех же единицах, что и радиус.
Если у вас площадь поверхности и радиус (r):
- Убедитесь, что поверхность и радиус указаны в тех же единицах , что и , а радиус указан в радианах.
- Вычтите 2πr² из площади поверхности.
- Разделите результата шага 1 на 2πr.
- Результат — высота цилиндра.
Как найти радиус цилиндра?
Если у вас объем и высота цилиндра:
- Убедитесь, что объем и высота указаны в тех же единицах (например, см³ и см), а радиус указан в радианах .
- Разделить объем на число пи и высота.
- Квадрат корень результата.
Если у вас есть площадь поверхности и высота (h):
- Подставьте высоту, h и площадь поверхности в уравнение, площадь поверхности = πr²h : 2πrh + 2πr².
- Разделите с обеих сторон на 2π.
- Вычтите площади поверхности/2π с обеих сторон.
- Решите полученное квадратное уравнение.
- Положительный корень — это радиус.
Как найти объем прямоугольного трапециевидного цилиндра?
Правильный трапециевидный цилиндр , также известный как прямоугольная призма , может быть решен следующим образом:
- Сложите вместе две параллельные стороны (основания) трапеции.
- Разделить результат на 2.
- Умножьте результат шага 2 на высоту трапеции (т.е. расстояние, разделяющее две стороны).
- Умножьте результат на длину цилиндра.
- Результатом является площадь прямоугольного трапециевидного цилиндра.
Как найти объем овального цилиндра?
Чтобы найти объем овального цилиндра:
- Умножьте наименьший радиус овала (малая ось) на его наибольший радиус (большая ось).
- Умножьте этого нового числа на пи .
- Разделите результат шага 2 на 4. Результатом будет площадь овала.
- Умножьте площадь овала на высоту цилиндра.
- Результат — объем овального цилиндра.
Как найти объем наклонного цилиндра?
Чтобы вычислить объем наклонного цилиндра:
- Найдите радиус , длину стороны и угол наклона цилиндра.
- Площадь радиус.
- Умножьте на число пи.
- Возьмем грех угла .
- Умножьте sin на длину стороны.
- Умножьте на результат шагов 3 и 5 вместе.
- В результате получается наклонный объем.
Как рассчитать рабочий объем цилиндра?
Чтобы вычислить рабочий объем цилиндра:
- Разделите диаметр отверстия на 2, чтобы получить радиус отверстия .


 Вместо прямоугольного конца у вас просто другая форма: круг для цилиндров, треугольник, шестиугольник или любой другой многоугольник для призмы.
Вместо прямоугольного конца у вас просто другая форма: круг для цилиндров, треугольник, шестиугольник или любой другой многоугольник для призмы.

 с одной осью и двумя параллельными кольцевыми основаниями, перпендикулярными общей оси цилиндров.
с одной осью и двумя параллельными кольцевыми основаниями, перпендикулярными общей оси цилиндров. Если вы хотите посчитать, сколько пластилина можно положить внутрь картонного рулона, воспользуйтесь стандартной формулой объема цилиндра — калькулятор посчитает в мгновение ока!
Если вы хотите посчитать, сколько пластилина можно положить внутрь картонного рулона, воспользуйтесь стандартной формулой объема цилиндра — калькулятор посчитает в мгновение ока!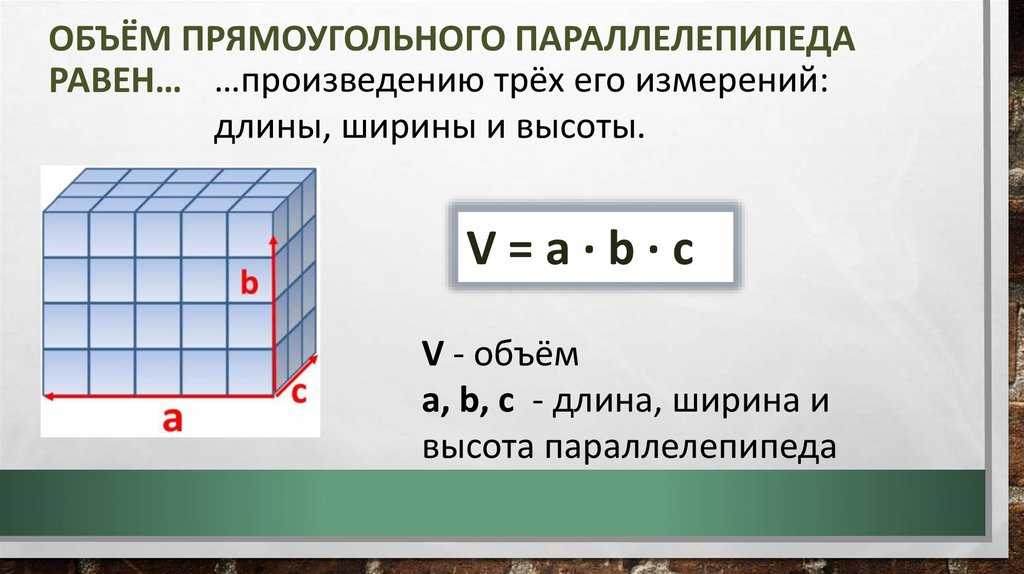 Хотя вещи в природе редко бывают идеальными цилиндрами, некоторые примеры стволы деревьев и стебли растений, некоторые кости (и, следовательно, тела) и жгутики микроскопических организмов. Они составляют большое количество природных объектов на Земле!
Хотя вещи в природе редко бывают идеальными цилиндрами, некоторые примеры стволы деревьев и стебли растений, некоторые кости (и, следовательно, тела) и жгутики микроскопических организмов. Они составляют большое количество природных объектов на Земле!